Quảng cáo
1 câu trả lời 167
a)
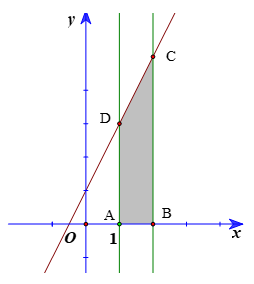
Gọi A(1; 0), B(2; 0) và C, D lần lượt là giao điểm của đường thẳng x = 2; x = 1 với đường thẳng y = 2x + 1. Khi đó C(2; 5), D(1; 3).
Tích phân cần tính chính là diện tích của hình thang vuông ABCD với đáy nhỏ AD = 3, đáy lớn BC = 5, đường cao AB = 1.
Khi đó \(\int\limits_1^2 {\left( {2x + 1} \right)dx} = {S_{ABCD}} = \frac{{\left( {AD + BC} \right)AB}}{2} = \frac{{\left( {3 + 5} \right).1}}{2} = 4\).
b)
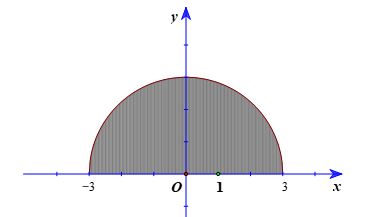
Ta có \(y = \sqrt {9 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx = \frac{1}{2}.\pi {.3^2} = \frac{9}{2}\pi \).
Quảng cáo
Bạn muốn hỏi bài tập?



