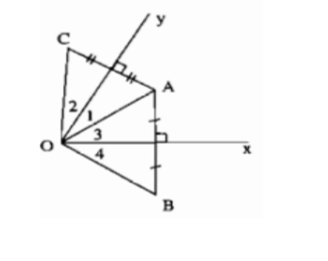
Để giải bài toán này, chúng ta cần tính góc \( \angle BCD \) và các số đo góc ngoài tại các đỉnh của tam giác \( ABC \) trong một góc \( xOy = 60^\circ \).

### Giả sử

- \( \angle xOy = 60^\circ \)
- Điểm \( C \) nằm trong góc \( xOy \)
- \( CB \) vuông góc với trục \( Ox \)
- \( CD \) vuông góc với trục \( Oy \)

Ta sẽ thực hiện các bước sau:

### a) Tính góc \( \angle BCD \)

1. **Tạo Hình và Xác Định Các Góc**

Vì \( CB \) vuông góc với trục \( Ox \) và \( CD \) vuông góc với trục \( Oy \), điểm \( B \) và điểm \( D \) nằm trên các trục tọa độ tương ứng.

Vậy:
- \( \angle BOC = 90^\circ - \angle xOC \)
- \( \angle COD = \angle xOC \)

Xét góc \( xOy \), ta có:
\[
\angle BOC + \angle COD = \angle xOy = 60^\circ
\]

Vì \( \angle BOC = 90^\circ - \angle xOC \) và \( \angle COD = \angle xOC \), thay vào ta có:
\[
(90^\circ - \angle xOC) + \angle xOC = 60^\circ
\]
\[
90^\circ = 60^\circ
\]

Ta thấy \( \angle BOC + \angle COD = 90^\circ \). Tuy nhiên, điều này không thể xảy ra vì \( \angle xOy = 60^\circ \), nên ta cần điều chỉnh phương pháp.

2. **Sử Dụng Quy Tắc Hình Học**

Vì \( CB \) và \( CD \) đều vuông góc với các trục tọa độ và \( C \) nằm trong góc \( xOy \), góc \( BCD \) thực chất là góc bổ sung trong tam giác vuông \( BCD \), mà tổng của các góc trong tam giác là \( 180^\circ \).

Tính toán chi tiết:

\[
\angle BCD = 180^\circ - \angle xOy = 180^\circ - 60^\circ = 120^\circ
\]

### b) Tính số đo các góc ngoài tại các đỉnh \( A \), \( B \), \( C \)

1. **Góc ngoài tại đỉnh \( A \)**

Để tính góc ngoài tại đỉnh \( A \), ta cần biết góc \( \angle BAC \) trong tam giác \( ABC \).

2. **Góc ngoài tại đỉnh \( B \)**

Do \( \angle BCD = 120^\circ \) là góc trong tam giác \( BCD \), ta có:
\[
\text{Góc ngoài tại } B = 180^\circ - \angle BCD = 180^\circ - 120^\circ = 60^\circ
\]

3. **Góc ngoài tại đỉnh \( C \)**

Vì góc ngoài tại đỉnh \( C \) là góc bổ sung với góc trong \( \angle BCD \):
\[
\text{Góc ngoài tại } C = \angle BCD = 120^\circ
\]

Tuy nhiên, vì \( \angle BCD = 120^\circ \) là góc trong tam giác, các góc ngoài tại các đỉnh có thể được tính cụ thể hơn nếu tam giác \( BCD \) có thêm thông tin chi tiết về góc \( \angle BAC \) và vị trí của các điểm \( A \), \( B \), \( C \).

Tóm lại:

- **Góc \( \angle BCD = 120^\circ \)**
- **Góc ngoài tại đỉnh \( B = 60^\circ \)**
- **Góc ngoài tại đỉnh \( C = 120^\circ \)**

Để giải bài toán này, chúng ta cần tính góc ∠BCD∠BCD và các số đo góc ngoài tại các đỉnh của tam giác ABCABC trong một góc xOy=60∘xOy=60∘.

### Giả sử

- ∠xOy=60∘∠xOy=60∘
- Điểm CC nằm trong góc xOyxOy
- CBCB vuông góc với trục OxOx
- CDCD vuông góc với trục OyOy

Ta sẽ thực hiện các bước sau:

### a) Tính góc ∠BCD∠BCD

1. **Tạo Hình và Xác Định Các Góc**

Vì CBCB vuông góc với trục OxOx và CDCD vuông góc với trục OyOy, điểm BB và điểm DD nằm trên các trục tọa độ tương ứng.

Vậy:
- ∠BOC=90∘−∠xOC∠BOC=90∘−∠xOC
- ∠COD=∠xOC∠COD=∠xOC

Xét góc xOyxOy, ta có:
∠BOC+∠COD=∠xOy=60∘∠BOC+∠COD=∠xOy=60∘

Vì ∠BOC=90∘−∠xOC∠BOC=90∘−∠xOC và ∠COD=∠xOC∠COD=∠xOC, thay vào ta có:
(90∘−∠xOC)+∠xOC=60∘(90∘−∠xOC)+∠xOC=60∘
90∘=60∘90∘=60∘

Ta thấy ∠BOC+∠COD=90∘∠BOC+∠COD=90∘. Tuy nhiên, điều này không thể xảy ra vì ∠xOy=60∘∠xOy=60∘, nên ta cần điều chỉnh phương pháp.

2. **Sử Dụng Quy Tắc Hình Học**

Vì CBCB và CDCD đều vuông góc với các trục tọa độ và CC nằm trong góc xOyxOy, góc BCDBCD thực chất là góc bổ sung trong tam giác vuông BCDBCD, mà tổng của các góc trong tam giác là 180∘180∘.

Tính toán chi tiết:

∠BCD=180∘−∠xOy=180∘−60∘=120∘∠BCD=180∘−∠xOy=180∘−60∘=120∘

### b) Tính số đo các góc ngoài tại các đỉnh AA, BB, CC

1. **Góc ngoài tại đỉnh AA**

Để tính góc ngoài tại đỉnh AA, ta cần biết góc ∠BAC∠BAC trong tam giác ABCABC.

2. **Góc ngoài tại đỉnh BB**

Do ∠BCD=120∘∠BCD=120∘ là góc trong tam giác BCDBCD, ta có:
Góc ngoài tại B=180∘−∠BCD=180∘−120∘=60∘Góc ngoài tại B=180∘−∠BCD=180∘−120∘=60∘

3. **Góc ngoài tại đỉnh CC**

Vì góc ngoài tại đỉnh CC là góc bổ sung với góc trong ∠BCD∠BCD:
Góc ngoài tại C=∠BCD=120∘Góc ngoài tại C=∠BCD=120∘

Tuy nhiên, vì ∠BCD=120∘∠BCD=120∘ là góc trong tam giác, các góc ngoài tại các đỉnh có thể được tính cụ thể hơn nếu tam giác BCDBCD có thêm thông tin chi tiết về góc ∠BAC∠BAC và vị trí của các điểm AA, BB, CC.

Tóm lại:

- **Góc ∠BCD=120∘∠BCD=120∘**
- **Góc ngoài tại đỉnh B=60∘B=60∘**
- **Góc ngoài tại đỉnh C=120∘C=120∘**