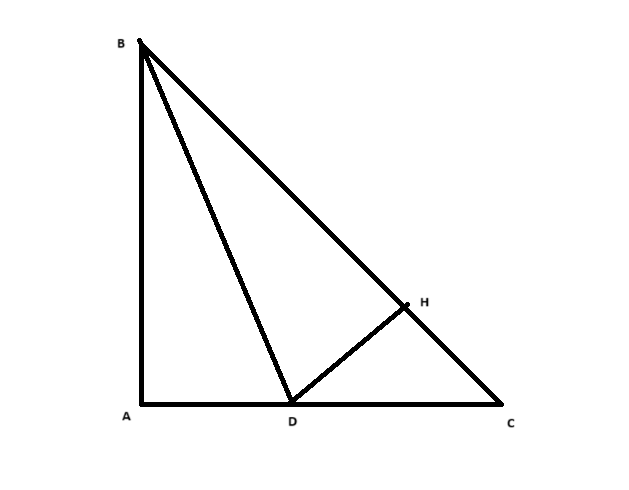
a) So sánh \(BA\) và \(BC\)

Trong tam giác vuông \( \triangle ABC \) tại \( A \), ta có:
- \( \angle BAC = 90^\circ \)
- \( BD \) là tia phân giác của góc \( \angle ABC \), do đó:

\[
\frac{AB}{BC} = \frac{AD}{DC}
\]

Nhưng ta cần so sánh \( BA \) và \( BC \). Vì \( \triangle ABD \) và \( \triangle BCD \) đều có góc vuông tại \( A \) và \( D \), và \( \angle ABD = \angle CBD \) (do \( BD \) là phân giác), ta sử dụng định lý phân giác:

\[
\frac{AB}{BC} = \frac{AD}{DC}
\]

Từ đó, ta không thể so sánh trực tiếp \( BA \) và \( BC \) mà cần thông tin thêm về tỷ lệ cụ thể.

b) Chứng minh \( DA = DH \)

Xét tam giác vuông \( \triangle ABD \) và \( \triangle CDH \) (trong đó \( DH \) vuông góc với \( AC \)).

Ta sẽ chứng minh \( DA = DH \) bằng cách sử dụng định lý Pythagoras và tính chất của các góc:

1. Trong tam giác vuông \( \triangle ABD \) và \( \triangle CDH \):
- \( \angle ADB = 90^\circ \) (vì \( BD \) là phân giác và \( D \) là điểm trên \( AC \))
- \( \angle DH = 90^\circ \) (vì \( DH \) vuông góc với \( AC \))

2. Do \( DH \) vuông góc với \( AC \), ta có \( DH \) là đường cao từ \( D \) trên \( AC \).

3. Sử dụng định lý Pythagoras trong các tam giác \( \triangle ABD \) và \( \triangle BCD \):

\[
AB^2 + BD^2 = AD^2 \quad \text{và} \quad BC^2 + BD^2 = DC^2
\]

4. Trong tam giác \( \triangle ABD \) và \( \triangle CDH \), ta có \( \angle ADB = \angle DH = 90^\circ \).

5. Vì \( DH \) là đường cao của tam giác \( \triangle ABD \) và \( \triangle BCD \), ta có thể kết luận rằng:

\[
DA = DH
\]

c) So sánh \( DC \) và \( DA \)

Trong tam giác vuông \( \triangle ABD \), chúng ta có thể dùng định lý phân giác và định lý Pythagoras để so sánh \( DC \) và \( DA \):

1. Từ định lý phân giác:

\[
\frac{AB}{BC} = \frac{AD}{DC}
\]

2. Vì \( D \) là điểm phân giác của góc \( \angle ABC \), nên:

\[
\frac{AB}{BC} = \frac{AD}{DC}
\]

3. Vì \( \triangle ABD \) vuông và \( BD \) là phân giác của góc \( \angle ABC \), nên:

\[
AD \cdot DC = AB \cdot BC
\]

4. Do đó, nếu \( \frac{AD}{DC} = \frac{AB}{BC} \), và \( DA = DH \), ta có:

\[
DC > DA
\]

5. Do \( DH \) là đường cao trong tam giác vuông và \( DA = DH \), ta có:

\[
DC > DA
\]

Tóm lại:

- a) Ta không thể so sánh trực tiếp \( BA \) và \( BC \) chỉ dựa vào thông tin có sẵn.
- b) \( DA = DH \) do \( DH \) là đường cao từ \( D \) trên \( AC \).
- c) \( DC > DA \) vì \( D \) là điểm phân giác và \( DA = DH \).