Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y = 2x3 – 3x2 + 1;
Quảng cáo
1 câu trả lời 755
a) y = 2x3 – 3x2 + 1
1) Tập xác định: ℝ.
2) Sự biến thiên:
Giới hạn tại vô cực: .
y' = 6x2 – 6x;
y' = 0 ⇔ 6x2 – 6x = 0 ⇔ x = 0 hoặc x = 1.
Bảng biến thiên:
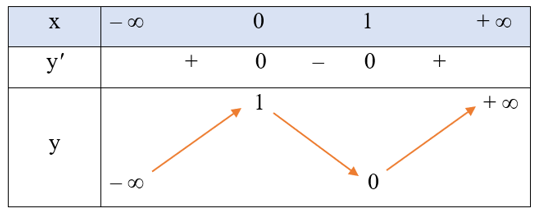
Hàm số đã cho đồng biến trên mỗi khoảng (– ∞; 0) và (1; + ∞); nghịch biến trên khoảng (0; 1).
Hàm số đạt cực đại tại x = 0, yCĐ = 1; đạt cực tiểu tại x = 1, yCT = 0.
3) Đồ thị
Giao điểm của đồ thị với trục tung: (0; 1).
Giao điểm của đồ thị với trục hoành:
Giải phương trình 2x3 – 3x2 + 1 = 0 ta được x = hoặc x = 1.
Vậy đồ thị hàm số giao với trục hoành tại các điểm , (1; 0).
Đồ thị hàm số đi qua các điểm (1; 0), (0; 1), , (– 1; – 4) và .
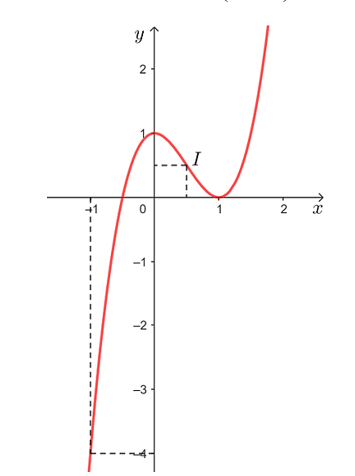
Vậy đồ thị hàm số y = 2x3 – 3x2 + 1 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I .
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



