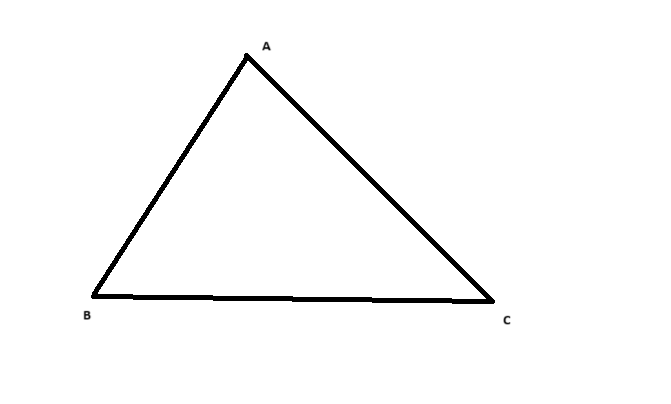
Để giải bài toán này, chúng ta sẽ sử dụng các công thức và định lý trong hình học hình tam giác.

Bước 1: Tính độ dài các cạnh AB và AC

Để tính độ dài các cạnh AB và AC, ta sẽ sử dụng định lý sin của tam giác:

\[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \]

Trong đó, \( a \), \( b \), \( c \) là độ dài các cạnh tương ứng với góc lần lượt là \( A \), \( B \), \( C \).

Given:
- \( B = 45^\circ \)
- \( C = 75^\circ \)
- \( BC = c = 5 \) (đây là cạnh giữa, tức là cạnh đối diện góc \( A \))

Tính AB:

\[ \frac{AB}{\sin 75^\circ} = \frac{5}{\sin 45^\circ} \]

Tính toán:
\[ \sin 75^\circ \approx 0.9659 \]
\[ \sin 45^\circ = \frac{\sqrt{2}}{2} \approx 0.7071 \]

\[ AB = \frac{5 \times 0.9659}{0.7071} \approx 6.856 \]

\[ AB \approx 6.86 \]

Tính AC:

\[ \frac{AC}{\sin 45^\circ} = \frac{5}{\sin 75^\circ} \]

Tính toán:
\[ \sin 75^\circ \approx 0.9659 \]
\[ \sin 45^\circ = \frac{\sqrt{2}}{2} \approx 0.7071 \]

\[ AC = \frac{5 \times 0.7071}{0.9659} \approx 3.66 \]

\[ AC \approx 3.66 \]

Bước 2: Tính bán kính đường tròn ngoại tiếp tam giác ABC

Bán kính \( R \) của đường tròn ngoại tiếp tam giác được tính bằng công thức sau đây:

\[ R = \frac{abc}{4S} \]

Trong đó:
- \( a, b, c \) là độ dài các cạnh của tam giác (đã tính được ở bước trên).
- \( S \) là diện tích tam giác ABC, được tính bằng công thức Heron khi biết các cạnh và góc:

\[ S = \frac{1}{2} ab \sin C \]

Với \( a = 6.856 \), \( b = 5 \), \( c = 3.66 \), \( C = 75^\circ \):

\[ S = \frac{1}{2} \times 6.856 \times 3.66 \times \sin 75^\circ \]

Tính toán \( S \):
\[ \sin 75^\circ \approx 0.9659 \]
\[ S \approx \frac{1}{2} \times 6.856 \times 3.66 \times 0.9659 \approx 12.84 \]

Sau đó, tính bán kính \( R \):
\[ R = \frac{6.856 \times 5 \times 3.66}{4 \times 12.84} \]
\[ R \approx \frac{125.718}{51.36} \approx 2.45 \]

Vậy, bán kính của đường tròn ngoại tiếp tam giác ABC là khoảng \( 2.45 \) (đơn vị chiều dài các cạnh tam giác).

Để giải bài toán này, chúng ta sẽ sử dụng các công thức và định lý trong hình học hình tam giác.

Bước 1: Tính độ dài các cạnh AB và AC

Để tính độ dài các cạnh AB và AC, ta sẽ sử dụng định lý sin của tam giác:

asinA=bsinB=csinC𝑎sin⁡𝐴=𝑏sin⁡𝐵=𝑐sin⁡𝐶

Trong đó, a𝑎, b𝑏, c𝑐 là độ dài các cạnh tương ứng với góc lần lượt là A𝐴, B𝐵, C𝐶.

Given:
- B=45∘𝐵=45∘
- C=75∘𝐶=75∘
- BC=c=5𝐵𝐶=𝑐=5 (đây là cạnh giữa, tức là cạnh đối diện góc A𝐴)

Tính AB:

ABsin75∘=5sin45∘𝐴𝐵sin⁡75∘=5sin⁡45∘

Tính toán:
sin75∘≈0.9659sin⁡75∘≈0.9659
sin45∘=√22≈0.7071sin⁡45∘=22≈0.7071

AB=5×0.96590.7071≈6.856𝐴𝐵=5×0.96590.7071≈6.856

AB≈6.86𝐴𝐵≈6.86

Tính AC:

ACsin45∘=5sin75∘𝐴𝐶sin⁡45∘=5sin⁡75∘

Tính toán:
sin75∘≈0.9659sin⁡75∘≈0.9659
sin45∘=√22≈0.7071sin⁡45∘=22≈0.7071

AC=5×0.70710.9659≈3.66𝐴𝐶=5×0.70710.9659≈3.66

AC≈3.66𝐴𝐶≈3.66

Bước 2: Tính bán kính đường tròn ngoại tiếp tam giác ABC

Bán kính R𝑅 của đường tròn ngoại tiếp tam giác được tính bằng công thức sau đây:

R=abc4S𝑅=𝑎𝑏𝑐4𝑆

Trong đó:
- a,b,c𝑎,𝑏,𝑐 là độ dài các cạnh của tam giác (đã tính được ở bước trên).
- S𝑆 là diện tích tam giác ABC, được tính bằng công thức Heron khi biết các cạnh và góc:

S=12absinC𝑆=12𝑎𝑏sin⁡𝐶

Với a=6.856𝑎=6.856, b=5𝑏=5, c=3.66𝑐=3.66, C=75∘𝐶=75∘:

S=12×6.856×3.66×sin75∘𝑆=12×6.856×3.66×sin⁡75∘

Tính toán S𝑆:
sin75∘≈0.9659sin⁡75∘≈0.9659
S≈12×6.856×3.66×0.9659≈12.84𝑆≈12×6.856×3.66×0.9659≈12.84

Sau đó, tính bán kính R𝑅:
R=6.856×5×3.664×12.84𝑅=6.856×5×3.664×12.84
R≈125.71851.36≈2.45𝑅≈125.71851.36≈2.45

Vậy, bán kính của đường tròn ngoại tiếp tam giác ABC là khoảng 2.452.45 (đơn vị chiều dài các cạnh tam giác).