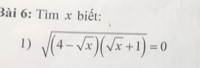4-xx+1=0 ???????

Anx Padascher Hỏi từ APP VIETJACK

Đã trả lời bởi chuyên gia

đã hỏi trong Lớp 7 Toán học

· 15:12 05/06/2024

Đã trả lời bởi chuyên gia

$\sqrt{(4 - \sqrt{x}) (\sqrt{x} + 1)} = 0$ ???????

Trả Lời (+5 điểm)

Lưu câu hỏi Lưu

Hỏi chi tiết

Quảng cáo

2 câu trả lời 226

Sang Phạm

1 năm trước

Để giải phương trình:

\[
\sqrt{4 - \sqrt{x}} \cdot (\sqrt{x} + 1) = 0
\]

Ta phân tích từng phần của phương trình này:

1. **Điều kiện của phương trình**:
- Để biểu thức có nghĩa, $ \sqrt{x} $ phải có nghĩa nên $ x \ge 0 $.
- $ 4 - \sqrt{x} $ phải không âm nên $ \sqrt{x} \le 4 $, tức là $ x \le 16 $.

Kết hợp lại, ta có điều kiện $ 0 \le x \le 16 $.

2. **Xét từng vế của phương trình**:
- $ \sqrt{4 - \sqrt{x}} = 0 $
- $ \sqrt{x} + 1 = 0 $

Chúng ta giải từng trường hợp một.

**Trường hợp 1**: $ \sqrt{4 - \sqrt{x}} = 0 $
- Khi đó $ 4 - \sqrt{x} = 0 $
- Suy ra $ \sqrt{x} = 4 $
- Bình phương hai vế: $ x = 16 $

Kiểm tra lại trong điều kiện ban đầu $ 0 \le x \le 16 $, giá trị $ x = 16 $ thỏa mãn điều kiện.

**Trường hợp 2**: $ \sqrt{x} + 1 = 0 $
- Khi đó $ \sqrt{x} = -1 $
- Do $ \sqrt{x} $ không bao giờ âm nên không có giá trị $ x $ nào thỏa mãn điều kiện này.

Vậy nghiệm duy nhất của phương trình là $ x = 16 $.

...Xem thêm

0 bình luận

1 ( 5.0 )

Đăng nhập để hỏi chi tiết