Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh = 5, độ dài cạnh bên = 20. Biết mặt phẳng (BCC'B') vuông góc với mặt đáy và góc B'BC = 30°. Tính thể tích khối chóp ACC'B'?
Quảng cáo
2 câu trả lời 1205
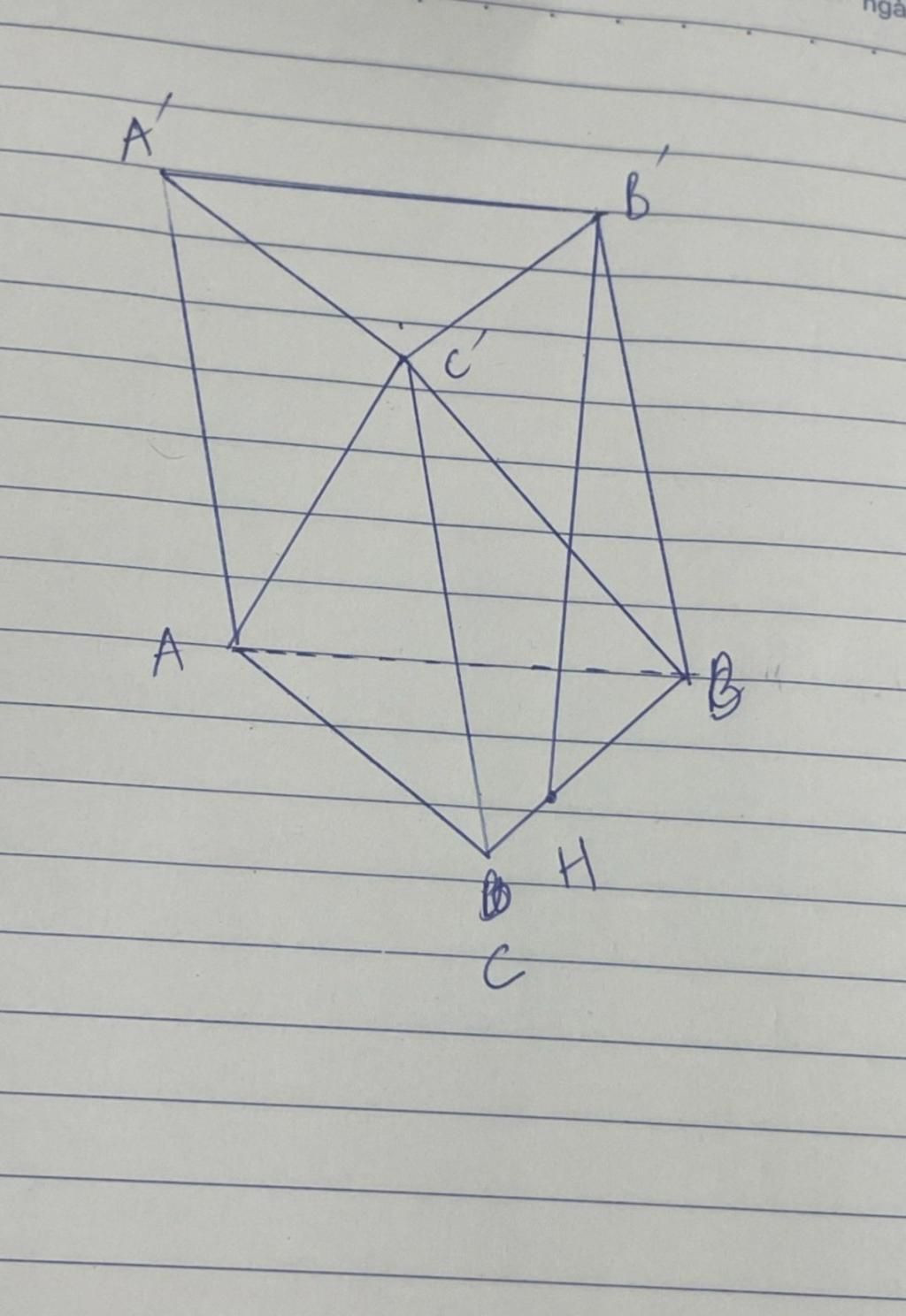
Có (BCC′B′)⊥(ABC)
(BCC′B)∩(ABC)=BC
Kẻ B'H⊥BC(H∈BC)
⇒B'H⊥(ABC)
ΔBB'H vuông tại H:
sinˆB′BH=BH'BB'
⇔sin30o=HB'20
⇒HB'=10
ΔABC đều cạnh 5
⇒S.ABC=25√34
V.ACC'B=V. C'ABC
=1/3.d(C'(ABC)).SABC
=1/3.d(B',(ABC)).SABC
=1/3.HB'.SABC
= 1/3.10.(25√3)/4≈36,1
Diện tích đáy của khối chóp $ACC'B'$ là:
$B = \frac{\sqrt{3}}{4}a^2 = \frac{\sqrt{3}}{4} \times 5^2 = \frac{25\sqrt{3}}{4}$
Thể tích khối chóp $ACC'B'$ là:
$V = \frac{1}{3} \times \frac{25\sqrt{3}}{4} \times 20 = \frac{25\sqrt{3}}{4} \times \frac{20}{3} = \frac{500\sqrt{3}}{3}$
=> Vậy ........
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134901
Đã trả lời bởi chuyên gia
134901 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76057
Đã trả lời bởi chuyên gia
76057 -
 Đã trả lời bởi chuyên gia
71711
Đã trả lời bởi chuyên gia
71711 -
 Đã trả lời bởi chuyên gia
47598
Đã trả lời bởi chuyên gia
47598
Gửi báo cáo thành công!


