a, chứng minh tam giác ABM bằng tam giác ACM
b, từ điểm M vẽ đường thẳng ME vuông góc với AB (E thuộc AB) , và vẽ đường thẳng MF vuông góc với AC (F thuộc AC) chứng minh ME=MF
Quảng cáo
2 câu trả lời 1463
a. Ta có tam giác ABC là tam giác cân tại đỉnh A, do đó AM là đường trung tuyến của tam giác ABC. Do tam giác ABC là tam giác cân nên AM là đường trung tuyến, nên \(AM\) chia \(BC\) thành hai đoạn bằng nhau, tức là \(BM = MC\).
Vậy, ta có:
\[
\begin{cases}
BM = MC \\
\angle BAM = \angle CAM \quad (\text{vì } AM \text{ là đường trung tuyến})
\end{cases}
\]
Do đó, theo trường hợp góc - cạnh - góc, ta suy ra tam giác \(ABM \cong ACM\) (cùng có một góc, cạnh chung và góc kề).
b. Ta có:
\[
\begin{cases}
BM = MC \\
\angle BME = \angle CMF = 90^\circ \quad (\text{do } ME \perp AB \text{ và } MF \perp AC)
\end{cases}
\]
Do tam giác \(ABM \cong ACM\), nên ta cũng có \(BE = CF\).
Vậy, ta có:
\[
\begin{cases}
BM = MC \\
BE = CF \\
\angle BME = \angle CMF = 90^\circ
\end{cases}
\]
Từ đó, ta suy ra \(ME = MF\) (hai tam giác \(BME\) và \(CMF\) đồng dạng, có cạnh góc vuông bằng nhau).
Như vậy, ta đã chứng minh được \(ME = MF\).
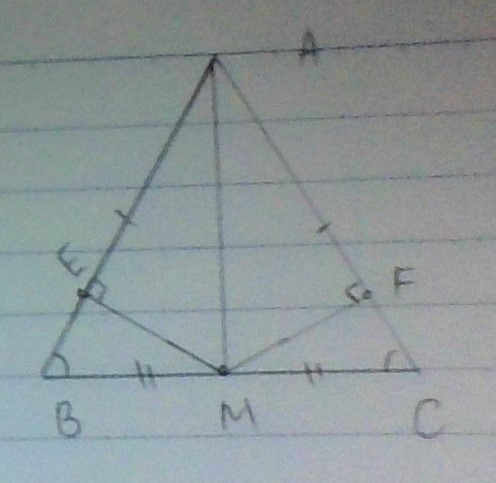
a) xét △ABM và △ACM có:
AB=AC (△ABC là △cân tại A)
BM=CM (AM là đg trug tuyến)
AM là cạnh chung
Vậy △ABM=△ACM (c.c.c)
b) xét △EBM(⊥ tại E)và △FCM(⊥ tại F) có:
BM=CM ( AM là đường trug tuyến)
góc B= góc C (△ABC cân)
Vậy△EBM=△FCM (cạnh huyền-góc nhọn)
=>ME=MF (2 cạnh tương ứng)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


