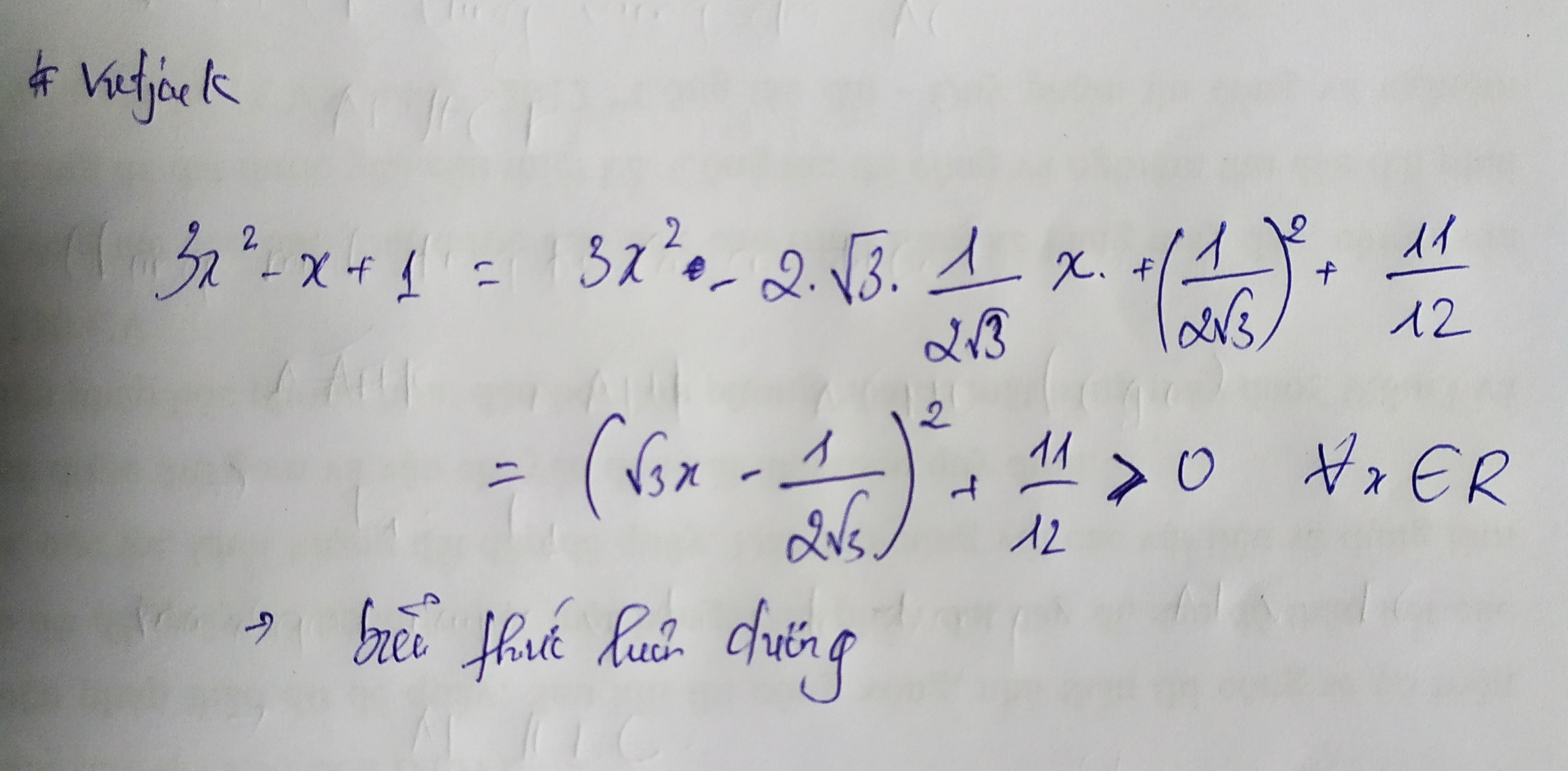3X2-x+1 xét dấu biểu thức
Quảng cáo
3 câu trả lời 969
$3x^2-x+1=x^2-\dfrac13 x+\dfrac13=x^2-\dfrac13 x+\dfrac1{36}+\dfrac{11}{36}$
$=\left(x-\dfrac16\right)^2+\dfrac{11}{36} \geq 0\; \forall x\in \mathbb{R}$
$\to$ Biểu thức luôn đúng
Để xét dấu biểu thức \(3x^2 - x + 1\), ta cần tìm các khoảng mà biểu thức này dương hoặc âm.
---
### Bước 1: Tìm discriminant (\(\Delta\))
\[
\Delta = b^2 - 4ac = (-1)^2 - 4 \times 3 \times 1 = 1 - 12 = -11
\]
### Bước 2: Xét dấu của biểu thức
- Vì \(\Delta < 0\), phương trình \(3x^2 - x + 1 = 0\) không có nghiệm thực.
- Dạng biểu thức \(ax^2 + bx + c\) với \(a > 0\) và \(\Delta < 0\), luôn dương với mọi \(x\).
---
### **Kết luận:**
\[
\boxed{
3x^2 - x + 1 > 0 \quad \text{với mọi } x \in \mathbb{R}
}
\]
Biểu thức luôn dương trên tập xác định.
---
Bạn cần gì thêm không?
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
✧
1915 điểm
-
I miss you
1475 điểm
-
bé ong của toiii 470 điểm
-
`d.`
290 điểm
-
đayy xoài 270 điểm
-
`color{blue}text{HuyTùng ✦``color{red}text{ ✦`
260 điểm
-
zai đẹp siu
220 điểm
-
✿ 𝓝𝓪̂́𝓶 🍄
175 điểm
-
minhxinhquama
155 điểm
-
(๑﹏๑//)☪ảทջՇɦàทɦđêℳƙɦôทջℳưα
140 điểm
-
(じんじんえｋ
135 điểm
-
Huong Nguyen 120 điểm
-
Haruto[pad] 120 điểm
-
Giaumy
120 điểm
Rút gọn
