a) chứng minh rằng: ∆ABC = ∆ DBC, từ đó suy ra BD vuông góc CD
b)Cho góc ABC = 60độ.Tính số đo góc ACD
Quảng cáo
1 câu trả lời 794
a) Ta cần chứng minh rằng \( \triangle ABC = \triangle DBC \).
Vì \( HD = HA \) và \( \angle HAD = \angle HDA = 90^\circ \) (vì \( AH \) vuông góc với \( BC \)), nên \( \triangle AHD \) là tam giác vuông cân tại \( H \).
Do đó, \( AD = HD = HA \).
Vậy, tam giác \( \triangle AHD \) và \( \triangle ABC \) là hai tam giác có cạnh \( AH \) chung và góc \( \angle AHD = \angle ABC = 90^\circ \) (do \( AH \) vuông góc với \( BC \)), và cạnh đối diện với góc đó bằng nhau (\( AD = HD = HA \)).
Vì vậy, theo tính chất của tam giác, ta có \( \triangle ABC = \triangle AHD \).
Tương tự, ta có \( \triangle AHD = \triangle DBC \) vì chúng có các cạnh và góc tương đương.
Từ đó, suy ra \( \triangle ABC = \triangle DBC \), và do đó, \( BD \) là đường cao của tam giác \( \triangle DBC \), nên \( BD \) vuông góc với \( CD \).
b) Với \( \angle ABC = 60^\circ \), ta có \( \angle AHD = 90^\circ \) (do \( AH \) vuông góc với \( BC \)), vì vậy \( \angle DHA = 180^\circ - 90^\circ - 60^\circ = 30^\circ \).
Như vậy, \( \angle ACD = \angle DHA = 30^\circ \).
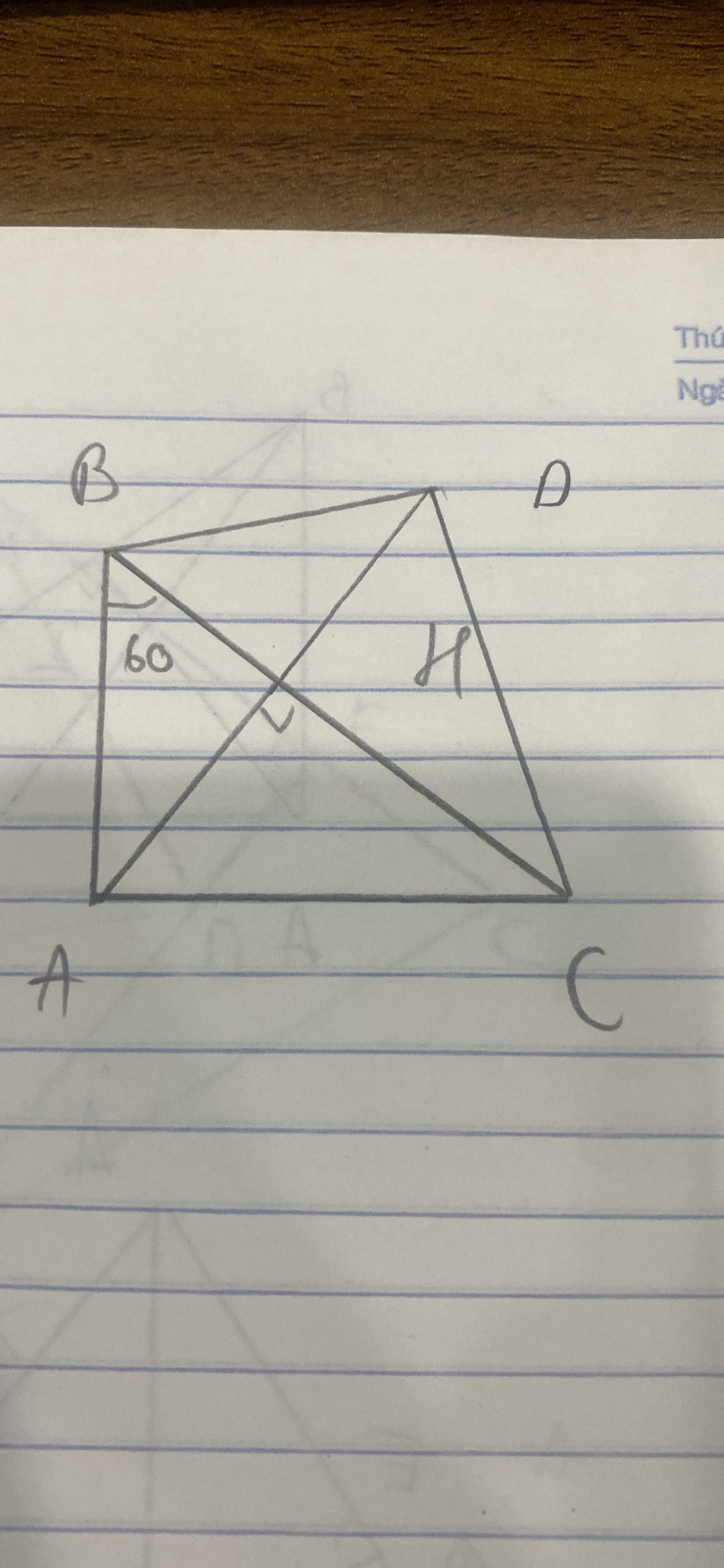
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


