Quảng cáo
2 câu trả lời 1497
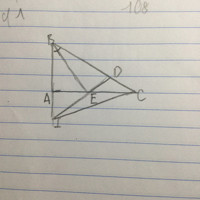
a) Ta có tam giác ABC và tam giác ABD cùng có góc A và góc B bằng nhau (AB = DB). Do đó, ta có tam giác ABC đồng dạng với tam giác ABD (theo định lí góc - cạnh - góc). Từ đó, ta có AE/AC = DE/DC. Nhưng ta cũng biết rằng AE = AC - EC và DE = DC - DC. Từ đó, ta có AC - EC/AC = DC - DC/DC. Tương đương với 1 - EC/AC = 1 - DC/DC. Do đó, EC = DC. Vậy ta có AE = DE.
b) Ta có tam giác ADE và tam giác AIB đồng dạng (theo định lí góc - cạnh - góc). Từ đó, ta có tg(AEI) = tg(DEC).
c) Ta có tam giác BCI và tam giác BAE đồng dạng (theo định lí góc - cạnh - góc). Từ đó, ta có góc BCI = góc BAE. Nhưng góc BAE = góc IAC (do AB cắt DE tại I). Vậy ta có góc BCI = góc IAC, từ đó suy ra BE vuông góc CI.
BE cạnh chung
Góc ABE = Góc DBE(BE là tia phân giác)
BA=BD(gt)
=>🔺BEA =🔺BEC(c-g-)
=>AE=ED(2 cạnh tương ứng)
b,Xét 🔺AEI và 🔺DEC có:
Góc AEI=Góc DEC (2 góc đối đỉnh)
Góc IAE=góc CDE(=90°)
=>🔺AEI=🔺DEC(cgv-gnk)
c,Từ cm câu a=>EI=EC
=>🔺EIC cân tại E
Mà 4 đường đi qua 🔺cân đều trùng nhau
=>BE vuông IC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


