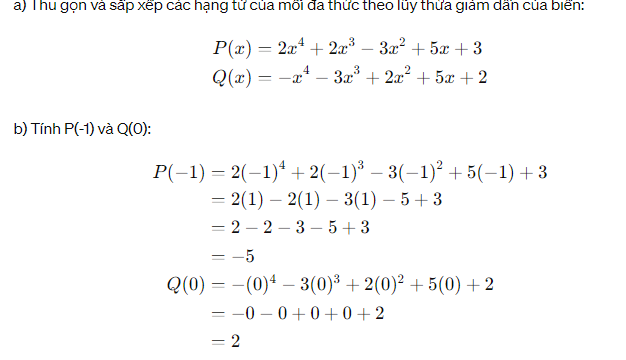Cho hai đa thức:
P(x) = 3x2 + 7 + 2x4 - 3x2 - 4 - 5x + 2x3
Q(x) = - 3x3 + 2x2 - x4 + x + x3 + 4x - 2 + 5x .
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biển.
b) Tính P(-1)và Q(0)
c )Tinh G(x) = P(x) + Q(x) .
d) Chứng tỏ rằng G(x) luôn dương với mọi giá trị của x.
Quảng cáo
2 câu trả lời 529
a) Thu gọn và sắp xếp các hạng tử:
P(x):
- Bỏ các hạng tử đồng dạng:
-` 3x^2 - 3x^2 = 0`
- `2x^3 + x^3 = 3x^3`
- `4 + 7 = 11`
- Sắp xếp theo lũy thừa giảm dần:
`P(x) = 2x^4 + 3x^3 + 2x^2 - 5x + 11`
Q(x):
- Bỏ các hạng tử đồng dạng:
- `-3x^3 + x^3 = 0`
`+ 2x^2 - x^2 = x^2`
`+ x + 4x = 5x`
`- 2 + 5x = 3x - 2`
- Sắp xếp theo lũy thừa giảm dần:
` Q(x) = -x^4 + x^2 + 5x - 2`
b) Tính P(-1) và Q(0):
P(-1):
- Thay x = -1 vào P(x):
`P(-1) = 2(-1)^4 + 3(-1)^3 + 2(-1)^2 - 5(-1) + 11`
`= 2 - 3 + 2 + 5 + 11`
`= 13`
Q(0):
- Thay x = 0 vào Q(x):
`Q(0) = -0^4 + 0^2 + 5(0) - 2`
` = 0 + 0 + 0 - 2`
` = -2`
c) Tính G(x) = P(x) + Q(x):
-` G(x) = P(x) + Q(x)`
`= (2x^4 + 3x^3 + 2x^2 - 5x + 11) + (-x^4 + x^2 + 5x - 2)`
`= x^4 + 4x^3 + 3x^2 + 0x + 9`
d) Chứng tỏ rằng G(x) luôn dương với mọi giá trị của x:
`- G(x) = x^4 + 4x^3 + 3x^2 + 0x + 9`
Phân tích các hạng tử:
- `x^4 ≥ 0` (với mọi x)
- `4x^3 ≥ 0` (với mọi x)
- `3x^2 ≥ 0` (với mọi x)
- `9 > 0`
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757