Question

Đã trả lời bởi chuyên gia

Answer 1

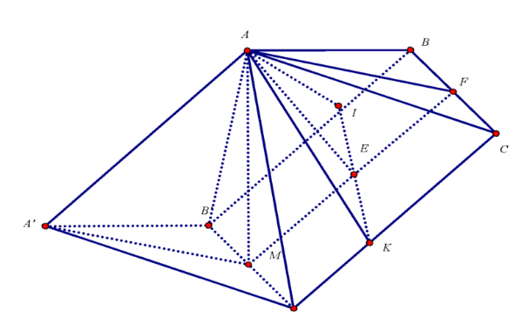
Kẻ AI ⊥ BB′, AK ⊥CC′ (hình vẽ).

Khoảng cách từ A đến BB′ và CC′ lần lượt là 1; 2

Þ AI = 1, AK = 2

Gọi F là trung điểm của BC.

Ta có: $A F = A' M = \frac{\sqrt{15}}{3}$

AI ⊥ BB′, BB’ ⊥ AK Þ BB’ ⊥ (AIK)

Hay BB’ ⊥ IK

Vì CC′ // BB′ ⇒ d(C, BB′) = d(K, BB′) = IK = $\sqrt{5}$

Þ ΔAIK vuông tại A.

Gọi E là trung điểm của IK

Þ EF // BB’

Þ EF ⊥ (AIK)

Þ EF ⊥ AE

Lại có: AM ⊥ (ABC)

Do đó góc giữa hai mặt phẳng (ABC) và (AIK) là góc giữa EF và AM

$\hat{A M E} = \hat{F A E}$

$\cos \hat{F A E} = \frac{A E}{A F} = \frac{\frac{\sqrt{5}}{2}}{\frac{\sqrt{15}}{3}} = \frac{\sqrt{3}}{2}$

$\Rightarrow \hat{F A E} = 30 °$

Hình chiếu vuông góc của tam giác ABC lên mặt phẳng (AIK) là ΔAIK nên ta có:

$S_{A I K} = S_{A B C} \cos \hat{E A F}$

$\Rightarrow S_{A B C} = \frac{2}{\sqrt{3}}$

Xét ΔAMF vuông tại A: $\tan \hat{A M F} = \frac{A F}{A M}$

$\Rightarrow A M = \frac{\frac{\sqrt{15}}{3}}{\frac{\sqrt{3}}{3}} = \sqrt{5} \Rightarrow V_{A B C . A^{'} B^{'} C^{'}} = \sqrt{5} . \frac{2}{\sqrt{3}} = \frac{2 \sqrt{15}}{3}$

Vậy $V_{A B C . A^{'} B^{'} C^{'}} = \frac{2 \sqrt{15}}{3}$ .

...Xem thêm

Answer 2