Đã trả lời bởi chuyên gia
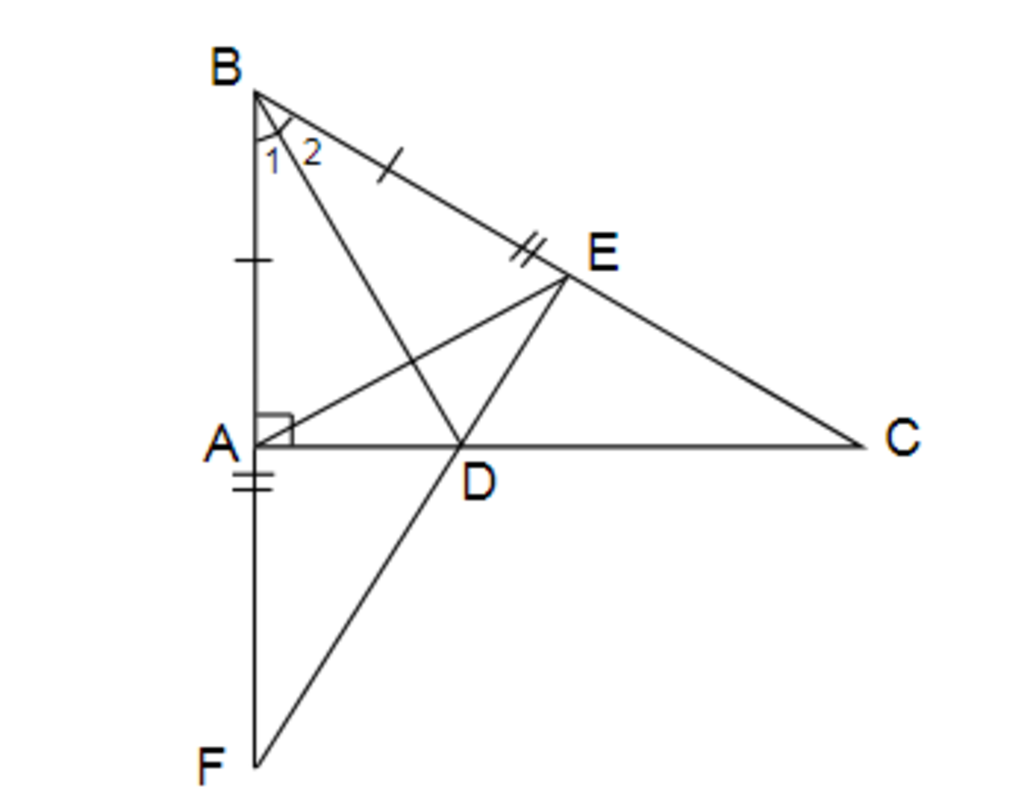
a.Tam giác ABD =tam giác EBD từ đó suy ra AD=ED
b.BD là đường trung trực của đoạn thẳng AE và AD<DC
c.Ba điểm E,D,F thẳng hàng
Quảng cáo
3 câu trả lời 4017
a)Xét ΔABD và ΔEBD có:
AB = EB (gt)
(theo gt)
BD: là cạnh chung
Vậy ΔABD = ΔEBD (c.g.c)
b, Δ DEC vuông tại E
⇒ DE < EC (cạnh góc vuông bé hơn cạnh huyền)
Mà DA = DE
Do đó: DA < DC.
c) Xét hai tam giác vuông ADF và EDC có:
DA = DE
Do đó: DA < DC.
⇒ ΔADF = ΔEDC
Hai đường cao AC và EF cắt nhau tại D
⇒ D là trực tâm của tam giác
nên D ∈ EF
Do đó: ba điểm E, D, F thẳng hàng (đpcm).
a. Ta có:
- Vì tam giác ABC vuông tại A nên $\angle BAC = 90^\circ$.
- Vì BE = BA nên tam giác ABE cũng là tam giác vuông tại E.
- Vì BF = BC nên tam giác BCF cũng là tam giác vuông tại F.
Khi đó, ta có $\angle ABE = 90^\circ - \angle BAE = 90^\circ - \angle BAC = \angle ABC$ và $\angle BCF = 90^\circ - \angle CBF = 90^\circ - \angle BAC = \angle ACB$.
Do đó, ta có $\angle ABE = \angle ABC = \angle ACB = \angle BCF$.
Vậy tam giác ABE và tam giác BCF đồng dạng, từ đó suy ra tam giác ABD = tam giác EBD (theo góc).
=>AD=ED
b. Ta có:
- Vì tam giác ABC vuông tại A nên $\angle ABC = 90^\circ$.
- Vì BD là tia phân giác của góc ABC nên $\angle ABD = \angle DBC$.
Từ đó, ta có $\angle ABD = \angle DBC = \angle ABC = 90^\circ$.
Vậy BD là đường trung trực của tam giác ABE.
a)Xét ΔABD và ΔEBD có:
AB = EB (gt)
ˆBAD=ˆBED (theo gt)
BD: là cạnh chung
Vậy ΔABD = ΔEBD (c.g.c)
b, Δ DEC vuông tại E
⇒ DE < EC (cạnh góc vuông bé hơn cạnh huyền)
Mà DA = DE
Do đó: DA < DC.
c) Xét hai tam giác vuông ADF và EDC có:
DA = DE
Do đó: DA < DC.
ˆADF=ˆEDC⇒ ΔADF = ΔEDC
Hai đường cao AC và EF cắt nhau tại D
⇒ D là trực tâm của tam giác
nên D ∈ EF
Do đó: ba điểm E, D, F thẳng hàng (đpcm).
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
Đã trả lời bởi chuyên gia
81971
-
Đã trả lời bởi chuyên gia
59862
-
Đã trả lời bởi chuyên gia
39757
-
cày 2000 điểm đổi tên 🥵
595 điểm
-
MINH__tu
495 điểm
-
🐟祖尼⚡
235 điểm
-
`color{blue}text{HuyTùng☢`
235 điểm
-
๖²⁴ʱČʉէε✦ɠїɾℓ༉ 185 điểm
-
meluynsu 🤗
160 điểm
-
devestro
115 điểm
-
𓇼 ⋆｡˚ 𓆝⋆｡˚ 𓇼
115 điểm
-
Phuong Hoàng 100 điểm
-
하루토 [팜 안 둥]
90 điểm
-
Huỳnh Lam Nguyên Huỳnh 85 điểm
-
너 없는 파리
80 điểm
-
보고 싶어요
65 điểm
-
muzik quang hùng
55 điểm
-
Ben 10K
50 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4999
