Question

Đã trả lời bởi chuyên gia

Answer 1

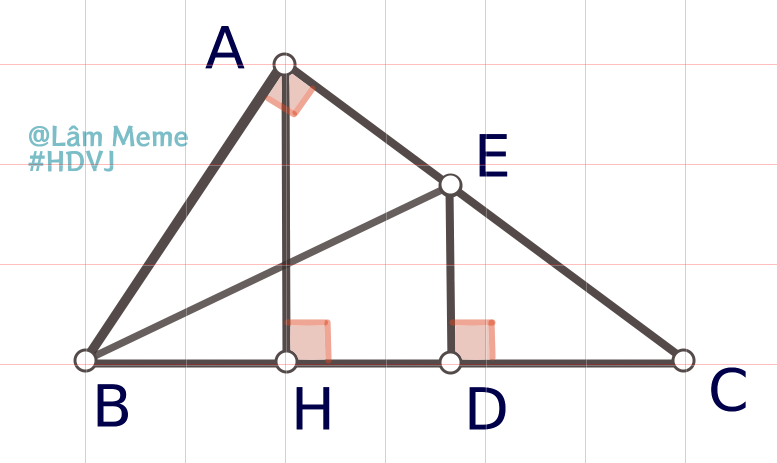
Xét `triangleABE` và `triangleDEB` có:

`hat{BAE}=hat{BDE}=90^o`

`BE` là cạnh chung

`BA=BD` (giả thiết)

`=>triangleABE=triangleDEB` (cạnh huyền -cạnh góc vuông)

Answer 2

Xét △ABE (vuông tại A) và △DEB (vuông tại D), có:

BE: cạnh chung

BA=BD (gt)

⇒ △ABE = △DEB (ch - cgv)

Answer 3

Chào bạn, đây là chứng minh cho bài toán hình học này:

📐 Chứng minh $\widehat{ABE} = \widehat{DBE}$
Để chứng minh $\widehat{ABE} = \widehat{DBE}$, ta sẽ chứng minh $\triangle \mathbf{ABE} = \triangle \mathbf{DBE}$.

1. Phân tích giả thiết và Cặp tam giác cần xét
Ta xét hai tam giác vuông tại A và D là $\triangle \mathbf{ABE}$ và $\triangle \mathbf{DBE}$.

$\triangle \mathbf{ABE}$ vuông tại $\mathbf{A}$ (vì $\triangle ABC$ vuông tại A).
$\triangle \mathbf{DBE}$ vuông tại $\mathbf{D}$ (vì $DE \perp BC$ tại D).
2. Chứng minh hai tam giác bằng nhau
Xét $\triangle \mathbf{ABE}$ (vuông tại A) và $\triangle \mathbf{DBE}$ (vuông tại D):

Cạnh huyền chung: $\mathbf{BE}$ là cạnh chung.
Cạnh góc vuông: Theo giả thiết, $\mathbf{BA = BD}$ (Cạnh góc vuông).
$\rightarrow$ Từ (1) và (2), suy ra:

$\triangle \mathbf{ABE} = \triangle \mathbf{DBE}$

(Trường hợp: Cạnh huyền - Cạnh góc vuông)

3. Kết luận
Vì $\triangle \mathbf{ABE} = \triangle \mathbf{DBE}$ (chứng minh trên), nên các góc tương ứng của chúng phải bằng nhau.

Do đó:

$\mathbf{\widehat{ABE} = \widehat{DBE}}$
(Điều phải chứng minh)

...Xem thêm

Answer 4