a) Chứng mình rằng H là trực tâm của Tam giác ABC
b) 3 điểm A, G, D thẳng hàng
Quảng cáo
2 câu trả lời 1147
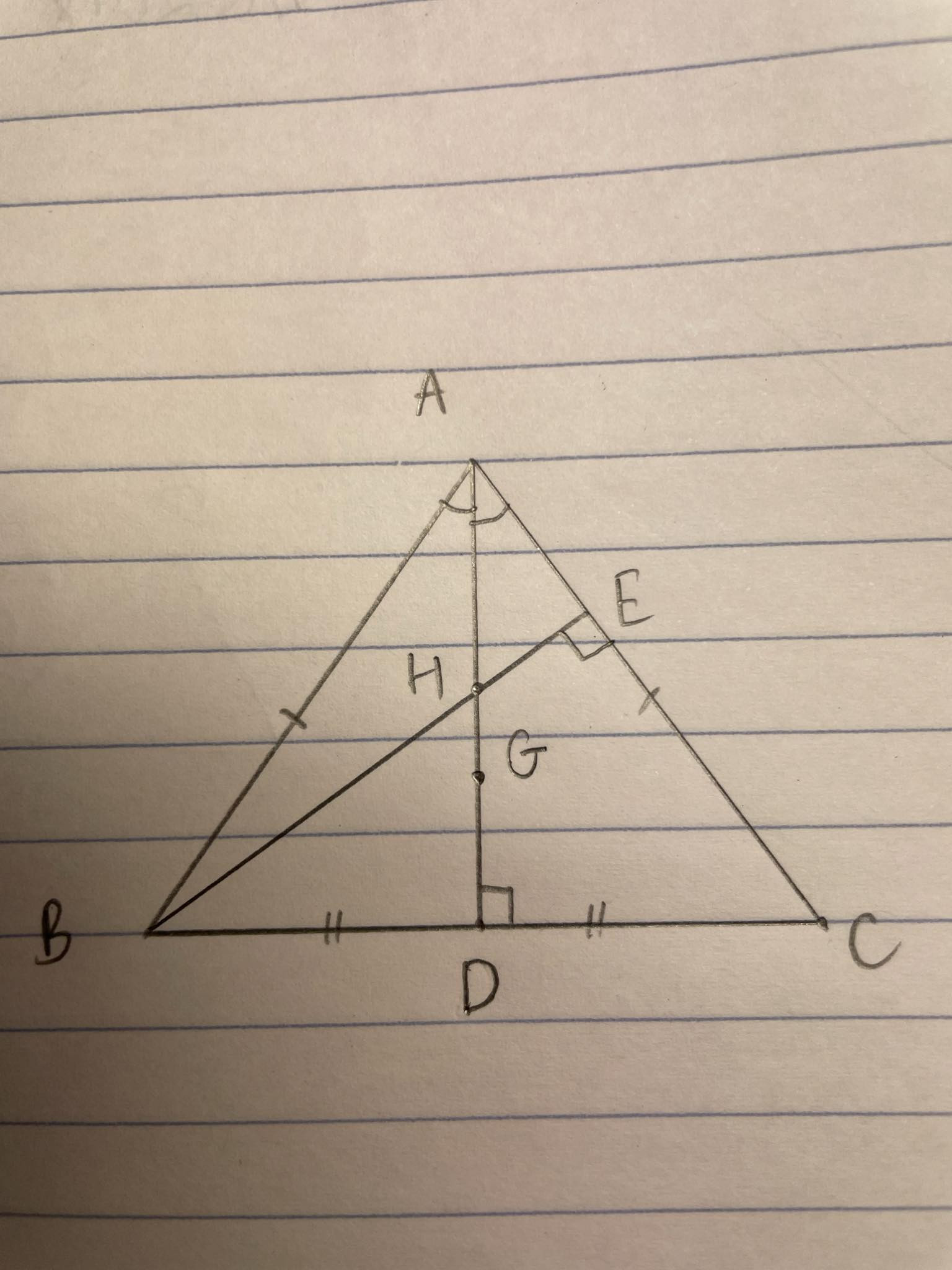
a)
Vì tam giác ABC là tam giác cân tại A, nên đường phân giác AD cũng là đường cao và đường trung tuyến của tam giác ABC. Do đó, ta có AH = HD.
Xét tam giác AHB, ta có:
AH = HD (vì AHB là tam giác cân)
∠AHB = ∠AHD (vì AB và AD là hai đường phân giác của tam giác ABC)
Do đó, tam giác AHB là tam giác cân và từ đó, ta có AH = HB.
Nên tam giác AHB là tam giác vuông cân tại H.
Vậy, H là trực tâm của tam giác ABC.
b)
Trọng tâm G chia đường phân giác AD thành tỉ lệ 2:1. Tức là AG = 2GD.
Vì tam giác ABC là tam giác cân, nên đường phân giác cũng là đường cao, từ đó ta có AH = HD.
Do đó, tổng AG + GD = AD = AH + HD.
Thay vào đó, ta có: AG + GD = AH + HD.
Nhưng ta đã biết rằng AH = HD và AG = 2GD.
Vậy, ba điểm A, G, D thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


