Cho tam giác ABC có AB > AC . Từ A kẻ AH vuông góc với BC ( H€ BC ) , trên đường thẳng AH lấy điểm M tùy ý . Chứng minh rằng :
a, góc BAH > góc CAH
b, BA > BM
a, góc BAH > góc CAH
b, BA > BM
Quảng cáo
2 câu trả lời 523
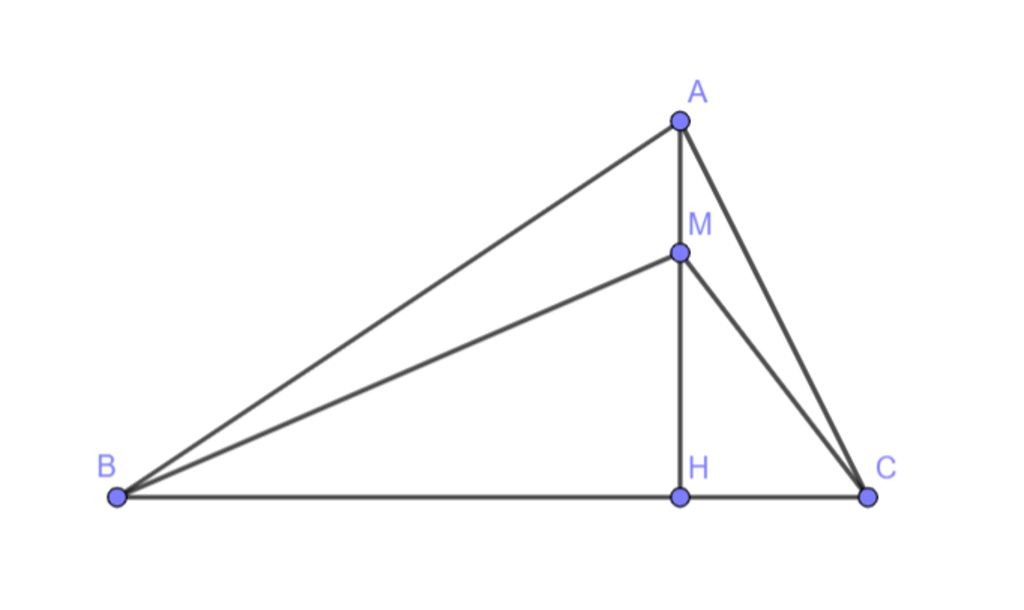
a)
Ta có:
AB > AC
nên
b)
M thuộc đoạn AH
⇒MH<AH
Mà:
MH là hình chiếu của BM trên AH
AH là hình chiếu của AB trên AH
⇒BM<AB.
a)
Ta có:
AB > AC
nên ˆB<ˆCB^<C^
Mà ˆBAH=90°−ˆB; ˆCAH=90°−ˆC⇒ˆBAH>ˆCAHMà BAH^=90°-B^; CAH^=90°-C^⇒BAH^>CAH^
b)
M thuộc đoạn AH
⇒MH<AH
Mà:
MH là hình chiếu của BM trên AH
AH là hình chiếu của AB trên AH
⇒BM<AB
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


