Quảng cáo
3 câu trả lời 373
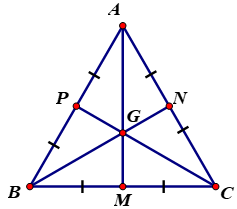
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
![]()
Từ (1) , (2) ⇒ GA = GB = GC.
Giả sử G là trọng tâm của tam giác đều ABC. Ta cần chứng minh rằng GA = GB = GC.
Vì tam giác ABC là tam giác đều nên ta có:
- AG = BG = CG (vì G là trọng tâm)
- G nằm trong tam giác ABC
Vậy ta đã chứng minh được rằng GA = GB = GC.
Giả sử G là trọng tâm của tam giác đều ABC. Ta cần chứng minh rằng GA = GB = GC.
Vì tam giác ABC là tam giác đều nên ta có:
- AG = BG = CG (vì G là trọng tâm)
- G nằm trong tam giác ABC
Vậy ta đã chứng minh được rằng GA = GB = GC.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


