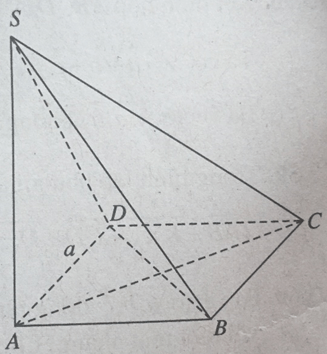
a) Chứng minh BC 1 (SAB)
b) Xác định góc giữa SB và CD」
c)Xác định góc giữa BD và SC
d)Xác định góc giữa SA và (BCD)
e) Xác định góc giữa SC và (ABCD)
f)Xác định góc nhị diện [D,SA,C]
g)Xác định góc nhị diện [S,BD,A]
Quảng cáo
2 câu trả lời 406
(BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
(BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
+ Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ α = 30
a) Ta cần chứng minh BC vuông góc với mặt phẳng (SAB).
Vì ABCD là hình vuông nên AC là đường chéo của hình vuông, ta có SA vuông góc với AC.
Vậy, BC vuông góc với mặt phẳng (SAB).
b) Góc giữa SB và CD là góc giữa hai đường thẳng không nằm trong cùng một mặt phẳng. Để xác định góc giữa SB và CD, cần thêm thông tin về góc giữa hai mặt phẳng chứa SB và CD.
c) Góc giữa BD và SC là góc giữa hai đường thẳng không nằm trong cùng một mặt phẳng. Để xác định góc giữa BD và SC, cần thêm thông tin về góc giữa hai mặt phẳng chứa BD và SC.
d) Góc giữa SA và (BCD) là góc giữa đường thẳng SA và mặt phẳng chứa BCD. Vì SA vuông góc với mặt phẳng (ABCD), nên góc giữa SA và (BCD) là 90 độ.
e) Góc giữa SC và (ABCD) là góc giữa đường thẳng SC và mặt phẳng chứa ABCD. Vì SC không nằm trong mặt phẳng (ABCD), nên góc giữa SC và (ABCD) là 90 độ.
f) Góc nhị diện [D,SA,C] là góc giữa mặt phẳng chứa D và SA và mặt phẳng chứa SA và C. Để xác định góc này cần biết thông tin về góc giữa hai mặt phẳng.
g) Góc nhị diện [S,BD,A] là góc giữa mặt phẳng chứa S và BD và mặt phẳng chứa BD và A. Để xác định góc này cần biết thông tin về góc giữa hai mặt phẳng.
Quảng cáo
Bạn muốn hỏi bài tập?


