Quảng cáo
2 câu trả lời 513
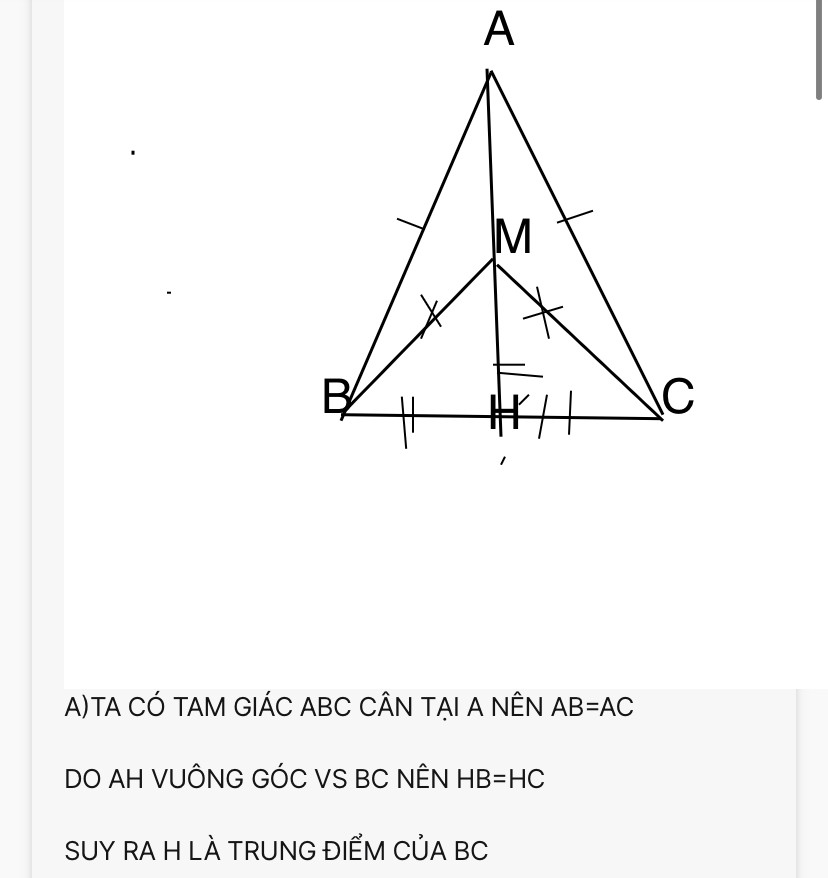
b, Giả sử BM ≠ BA. Khi đó, tam giác ABM không cân. Ta sẽ chứng minh điều này bằng phản chứng.
Vì BM ≠ BA, nên tam giác ABM không cân. Khi đó, AH sẽ là đoạn đối diện với góc ABC và AM sẽ là đoạn đối diện với góc BAC trong tam giác ABM.
Theo định lý cosin trong tam giác ABM:
\[BM^2 = BA^2 + AM^2 - 2 \cdot BA \cdot AM \cdot \cos(\angle BAC)\]
Vì góc ABC và góc BAC bằng nhau (vì tam giác ABC cân tại A), nên \(\cos(\angle BAC) = \cos(\angle ABC)\).
Nhưng ta cũng có:
\[BH^2 = BA^2 + AH^2 - 2 \cdot BA \cdot AH \cdot \cos(\angle ABC)\]
Vì AH vuông góc với BC, nên \(\cos(\angle ABC) = 0\).
Do đó, phương trình trở thành:
\[BH^2 = BA^2 + AH^2\]
Nhưng \(BH = CH\) vì tam giác ABC cân tại A. Do đó, \(CH^2 = BA^2 + AH^2\).
Điều này đồng nghĩa với việc \(BH^2 = CH^2\), nhưng vì BH và CH đều là độ dài dương, nên \(BH = CH\).
a, Ta có tam giác ABC cân tại A nên BH = CH (do đường cao từ đỉnh của tam giác cân xuống đáy là đối xứng với đường trung tuyến qua đỉnh).
b, Ta có tam giác ABC cân tại A nên AM là đường cao của tam giác ABC nên AM vuông góc với BC. Do đó, tam giác ABM vuông tại M.
Khi đó, ta có: BA = BM (theo tính chất của tam giác vuông).
# thi tốt nha
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


