Cho hình bình hành ABCD có BC = 2AB. Gọi M, N lần lượt là trung điểm của BC, AD.
Tìm điều kiện của hình bình hành ABCD để tứ giác PMQN là hình vuông.
Quảng cáo
1 câu trả lời 219
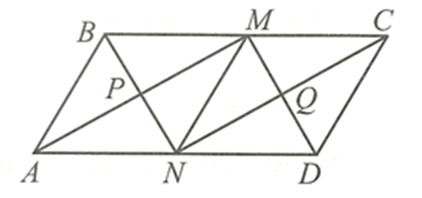
Để hình chữ nhật PMQN là hình vuông thì PM = PN.
Mà ABMN là hình thoi nên ABMN cũng là hình bình hành.
Suy ra AM, BN cắt nhau tại trung điểm P của mỗi đường.
Mà PM = PN, suy ra AM = BN.
Hình bình hành ABMN có AM = BN nên ABMN là hình chữ nhật.
Suy ra \(\widehat {ABM} = 90^\circ \) hay \(\widehat {ABC} = 90^\circ \).
Hình bình hành ABCD có \(\widehat {ABC} = 90^\circ \) nên ABCD là hình chữ nhật.
Dễ thấy, nếu hình bình hành ABCD là hình chữ nhật và BC = 2AB thì PMQN là hình vuông.
Vậy điều kiện của hình bình hành ABCD để PMQN là hình vuông là hình bình hành ABCD là hình chữ nhật có BC = 2AB.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


