a) CMR: tam giác AMN cân tại A
b) Vẽ P sao cho H là trung điểm NP CMR: BC là đường trung trực MP
c) MP cắt BC tại K, NK cắt MH tại D . CMR: AH,MN,DP đồng quy
Quảng cáo
4 câu trả lời 1358
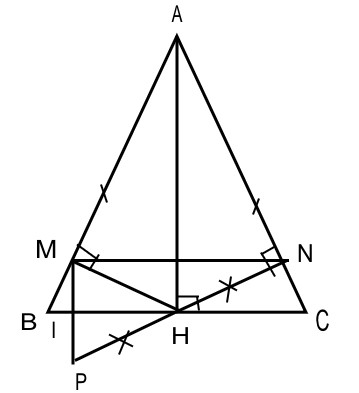
a)
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
Do đó: ΔBMH=ΔCNH (g.c.g)
nên BM=CN
=>AM=AN
hay ΔAMN cân tại A
b)
Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 90o (phụ nhau)
góc AHN + góc NHC = 90o (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng)
=> I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 180o
=> 2.góc MIH = 180o
=> góc MIH = 180o : 2
=> góc MIH = 90o
=> HI ⊥MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạn thẳng MP (Đpcm)
c)
Trong tam giác ΔMNP có :
MH;NK là hai đường trung tuyến lần lượt xuất phát từ đỉnh M và N.
Mà NK cắt MH tại điểm D (gt)
⇒D là trọng tâm của tam giác MNP
Lại có : O là trung điểm của MN
do đó : PO là đường trung tuyến xuất phát từ đỉnh P
⇒PD đi qua O. (*)
Mặt khác :
O là giao điểm của AH với MN. (**)
Từ (*) và (**) suy ra : ba đường thẳng AH;MN;DP cùng đi qua 1 điểm đó là điểm O. (đpcm)
a)
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
ˆB=ˆCB^=C^
Do đó: ΔBMH=ΔCNH (g.c.g)
nên BM=CN
=>AM=AN
hay ΔAMN cân tại A
b)
Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 90o (phụ nhau)
góc AHN + góc NHC = 90o (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng)
=> I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 180o
=> 2.góc MIH = 180o
=> góc MIH = 180o : 2
=> góc MIH = 90o
=> HI ⊥MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạn thẳng MP (Đpcm)
c)
Trong tam giác ΔMNP có :
MH;NK là hai đường trung tuyến lần lượt xuất phát từ đỉnh M và N.
Mà NK cắt MH tại điểm D (gt)
⇒D là trọng tâm của tam giác MNP
Lại có : O là trung điểm của MN
do đó : PO là đường trung tuyến xuất phát từ đỉnh P
⇒PD đi qua O. (*)
Mặt khác :
O là giao điểm của AH với MN. (**)
Từ (*) và (**) suy ra : ba đường thẳng AH;MN;DP cùng đi qua 1 điểm đó là điểm O. (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


