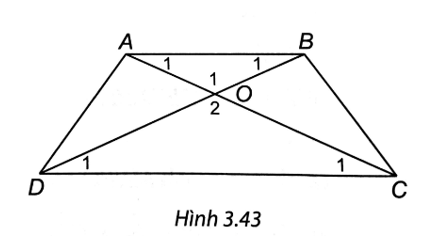
Chứng minh rằng nếu nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.43).
Quảng cáo
1 câu trả lời 151
1 năm trước
Xét tứ giác ABCD đó có hai đường chéo AC = BD, hai cạnh đối AD = BC.
Hai tam giác ABD và BCA có: cạnh chung AB, AC = BD, AD = BC.
Vậy ∆ABD = ∆BCA (c.c.c).
⇒ (1)
Tương tự, ta có ∆ACD = ∆BDC (c.c.c)
⇒ (2)
Gọi O là giao của hai đường chéo AC và BD thì (hai góc đối đỉnh). (3)
Từ (1), (2), (3), ta có ⇒ AB // CD ⇒ ABCD là hình thang.
Vậy hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!


