Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC.
Chứng minh tứ giác DEFG là một hình vuông.
Quảng cáo
1 câu trả lời 149
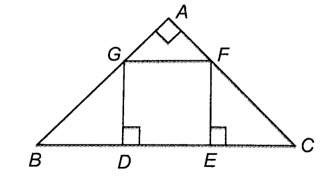
Do ∆ABC vuông cân tại A nên .
Xét ∆GBD vuông tại D và ∆EFC vuông tại E có:
BD = EC;
Do đó ∆GBD = ∆FCE (cạnh góc vuông – góc nhọn kề)
Suy ra
Mà nên
Do đó
Suy ra ∆GBD vuông cân tại D và ∆EFC vuông cân tại E.
Vì vậy GD = BD, EF = EC.
Mà
Suy ra GD = DE = EF.
Do GD ⊥ BC, EF ⊥ BC nên GD // EF
Tứ giác GDEF có GD // EF, GD = EF nên GDEF là hình chữ nhật.
Lại có GD và DE là hai cạnh kề của hình chữ nhật GDEF bằng nhau nên GDEF là hình vuông.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


