Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
Quảng cáo
1 câu trả lời 84
1 năm trước
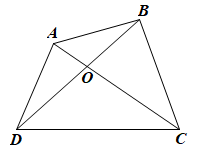
Xét tứ giác ABCD. Chu vi tứ giác ABCD là PABCD = AB + BC + CD + DA.
a) Trong ∆ABC có AC < AB + BC (bất đẳng thức trong tam giác)
Trong ∆ACD có AC < CD + DA (bất đẳng thức trong tam giác)
Do đó AC + AC < AB + BC + CD + DA hay 2AC < PABCD (1)
Tương tự, trong ∆ABD có BD < AD + AB
Trong ∆BCD có: BD < CD + BC
Do đó BD + BD < AD + AB + CD + BC hay 2BD < PABCD. (2)
Từ (1) và (2) suy ra 2(AC + BD) < 2PABCD, do đó AC + BD < PABCD.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!


