Với hai điểm phân biệt A, B cố định và phân biệt. Một đường thẳng l thay đổi luôn đi qua A và cách B một khoảng \(\frac{{AB}}{2}\). Gọi H là hình chiếu của B lên l. Tập hợp điểm H là
A. Một mặt phẳng;
B. Một mặt trụ;
C. Một mặt nón;
D. Một đường tròn.
Quảng cáo
1 câu trả lời 74
1 năm trước
Lời giải
Đáp án đúng là: D
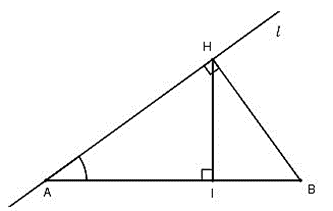
\(\sin \widehat {HAB} = \frac{{BH}}{{AB}} = \frac{1}{2} \Rightarrow \widehat {HAB} = 30^\circ \)
Tập hợp l là mặt nón có trục AB, đường sinh l, góc ở đỉnh là 60°
Gọi I là hình chiếu của H lên AB
Ta có: \(BI = BH\,.\,\cos 60^\circ = \frac{{AB}}{4}\) Þ I cố định.
Lại có \(IH = BH\,.\,\sin 60^\circ = \frac{{AB}}{2}\,.\,\frac{{\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{4}\).
Do đó H luôn cách I một khoảng bằng \(\frac{{AB\sqrt 3 }}{4}\) không đổi.
Vậy tập hợp điểm H là một đường tròn tâm I bán kính \(\frac{{AB\sqrt 3 }}{4}\).
Chọn đáp án D.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272
Gửi báo cáo thành công!



