Quảng cáo
4 câu trả lời 4920
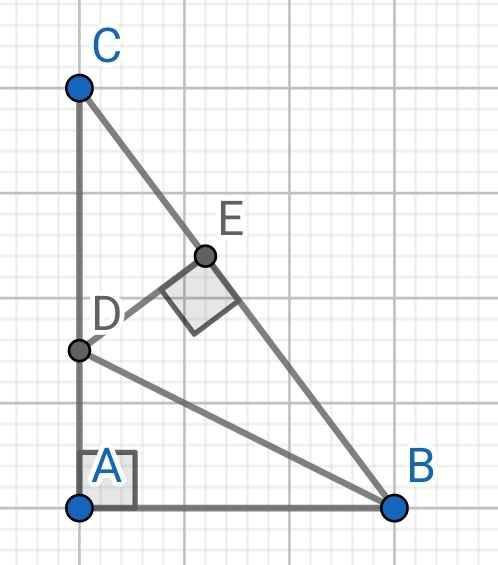
a)
Do BD là tia phân giác của ABC^ (gt)
Xét hai tam giác vuông ∆ABD và ∆EBD có:
BD là cạnh chung
(cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
b) BD là cạnh huyền của tam giác vuông BDE
=> BD > DE
Chứng minh:
a) Tam giác ABD = EBD:
Cạnh AB chung
Góc ABD = EBD:BD là phân giác của góc ABC (gt)
=> Góc ABD = Góc EBD (tính chất phân giác)
Cạnh BD chung
=> Tam giác ABD = EBD (c.g.c)
b) Chứng minh DB > DE:
Cách 1:
Sử dụng tính chất tam giác cân:
Tam giác ABD = EBD (cmt)
=> AD = DE (hai cạnh tương ứng)
Xét tam giác vuông ADE:
AD > DE (cạnh huyền lớn hơn cạnh góc vuông)
Cách 2:
Sử dụng định lý cosin:
Trong tam giác ABC:
BC^2 = AB^2 + AC^2
BC^2 = 3^2 + 4^2
BC^2 = 25
BC = 5 (cm)
Trong tam giác ABD:
BD^2 = AB^2 + AD^2
BD^2 = 3^2 + AD^2
Trong tam giác EBD:
BD^2 = BE^2 + DE^2
BD^2 = BE^2 + DE^2
Vì AD = DE (cmt) và BD^2 = BD^2:
=> BE^2 > AD^2
=> BE > AD
Mà BE = BC - CE và AD = AC - CD:
=> BC - CE > AC - CD
=> CE < CD
Xét tam giác vuông BCE và tam giác vuông ACD:
Góc BCE = Góc ACD (góc đối đỉnh)
BC = AC (gt)
CE < CD (cmt)
=> Tam giác BCE < Tam giác ACD
=> BE < AD (cạnh huyền tương ứng)
Mâu thuẫn với BE > AD (cmt)
Vậy kết luận DE < DB là sai.
Kết luận:
Tam giác ABD = EBD (cmt)
Do không đủ dữ liệu để so sánh DE và DB, nên không thể khẳng định DB > DE.
xet tg abd và tg ebd có BAD=90 =BED=90 độ
Bd chug
ABD=DBE (bd là phân giác ) suy ra (g.cg)
câu b sai đề ak
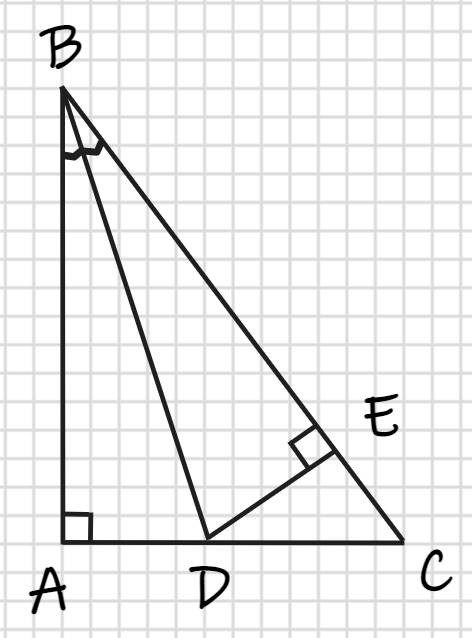
a: Xét ΔABD vuông tại A và ΔEBD vuông tại A có
BD chung
ABD^=EBD^ABD=EBD
Do đó: ΔBAD=ΔBED
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


