Cho tam giác ABC vuông tại A (AB < AC). Gọi E là trung điểm của BC. Từ E lần lượt kẻ ED vuông góc AC tại D, EF vuông góc với AB tại F.
a) Chứng minh tứ giác ADEF là hình chữ nhật.
b) Gọi K là điểm đối xứng của E qua F. Chứng minh tứ giác AEBK là hình thoi.
Quảng cáo
1 câu trả lời 419
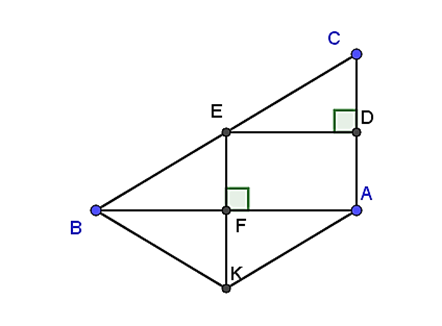
a)
Xét tứ giác ADEF
\(\begin{array}{l}\widehat A = 90^\circ \\\widehat {ADE} = 90^\circ \\\widehat {EFA} = 90^\circ \end{array}\)
Do đó, ADEF là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật).
b)
Xét tam giác CBA có:
E là trung điểm của BC (gt)
EF song song với CA (do EF song song với AD, C thuộc DA)
Do đó, F là trung điểm của AB (định lý về đường trung bình của tam giác)
Xét tứ giác AEBF có
F là trung điểm của đường chéo AB(cmt)
F là trung điểm của đường chéo EK(do E và K đối xứng nhau qua F)
Do đó: AEBF là hình bình hành(dấu hiệu nhận biết hình bình hành)
mà EK vuông góc với AB (do EF vuông góc với AB, K thuộc EF)
nên AEBF là hình thoi(dấu hiệu nhận biết hình thoi).
Quảng cáo
Bạn muốn hỏi bài tập?



