Quảng cáo
1 câu trả lời 390
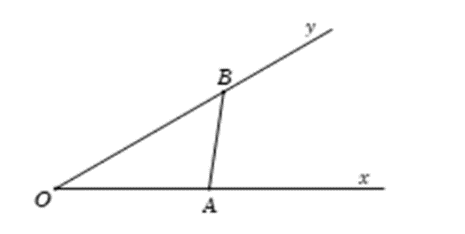
Theo định lý hàm sin, ta có:
\[\frac{{OB}}{{\sin \widehat {OAB}}} = \frac{{AB}}{{\sin \widehat {AOB}}}\]
\[ \Leftrightarrow OB = \frac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB}\]
\[ = \frac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\]
Do đó, độ dài OB lớn nhất khi và chỉ khi \[\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \]
Khi đó OB = 2
Tam giác OAB vuông tại A
\[ \Rightarrow OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \]
Đáp án cần chọn là: B
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340
Gửi báo cáo thành công!



