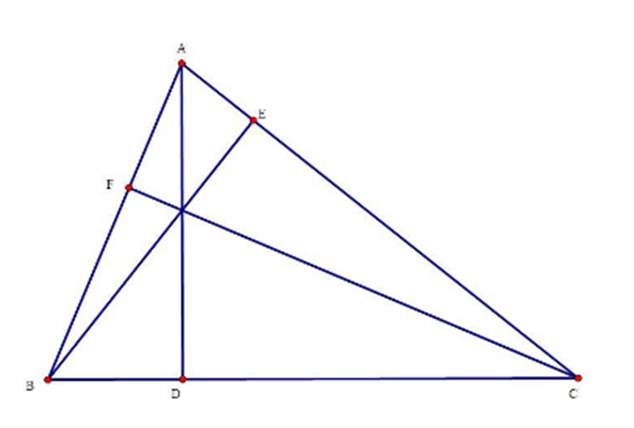
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh rằng: \(\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}} \ge \sqrt 3 \).
Quảng cáo
1 câu trả lời 105
\[{\left( {\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}}} \right)^2} \ge 3\sqrt {\frac{{HA}}{{BC}}.\frac{{HB}}{{AC}} + \frac{{HB}}{{AC}}.\frac{{HC}}{{AB}} + \frac{{HC}}{{AB}}.\frac{{HA}}{{BC}}} \](*)
Xét tam giác HAE và tam giác CAD có:
Chung \(\widehat A\)
\(\widehat {CDA} = \widehat {AEH}\)
⇒ ∆HAE ᔕ ∆CAD (g.g)
⇒ \(\frac{{HA}}{{CA}} = \frac{{AE}}{{AD}}\)
⇒\(\frac{{HA.HB}}{{CA.CB}} = \frac{{AE.HB}}{{AD.CB}} = \frac{{{S_{AHB}}}}{{{S_{ABC}}}}\)(1)
Tương tự ta có:
\(\frac{{HB.HC}}{{AB.AC}} = \frac{{{S_{AHC}}}}{{{S_{ABC}}}}\)(2)
\(\frac{{HC.HA}}{{BC.BA}} = \frac{{{S_{BHC}}}}{{{S_{ABC}}}}\)(3)
Cộng (1), (2), (3) theo từng vế ta có:
\(\frac{{HA.HB}}{{CA.CB}} + \frac{{HB.HC}}{{AB.AC}} + \frac{{HC.HA}}{{BC.BA}} = \frac{{{S_{AHB}}}}{{{S_{ABC}}}} + \frac{{{S_{AHC}}}}{{{S_{ABC}}}} + \frac{{{S_{BHC}}}}{{{S_{ABC}}}} = 1\)(**)
Từ (*) và (**) ta có: \[{\left( {\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}}} \right)^2} \ge 3\sqrt 1 = 3\]
Hay \(\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}} \ge \sqrt 3 \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



