Cho tam giác ABC có BC = 12cm, \(\widehat B\)= 60°, \(\widehat C\)= 40°. Tính: Đường cao CH và cạnh AC.
Quảng cáo
1 câu trả lời 74
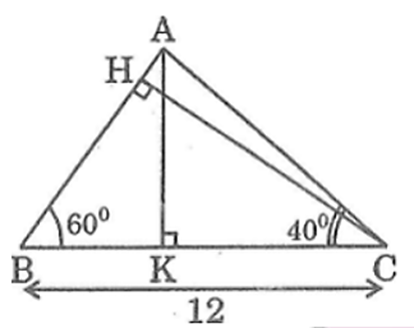
Trong tam giác BCH vuông, ta có:
CH = BC . sin \(\widehat B\) = 12 . sin 60° ≈ 10,392 (cm).
Trong tam giác ABC, ta có:
\(\widehat A\)= 180° – 60° – 40° = 80°
Trong tam giác ACH vuông, ta có:
AC = \(\frac{{CH}}{{\sin \left( {\widehat A} \right)}} \approx \frac{{10,392}}{{\sin \left( {80^\circ } \right)}}\)= 10,552 (cm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393
Gửi báo cáo thành công!



