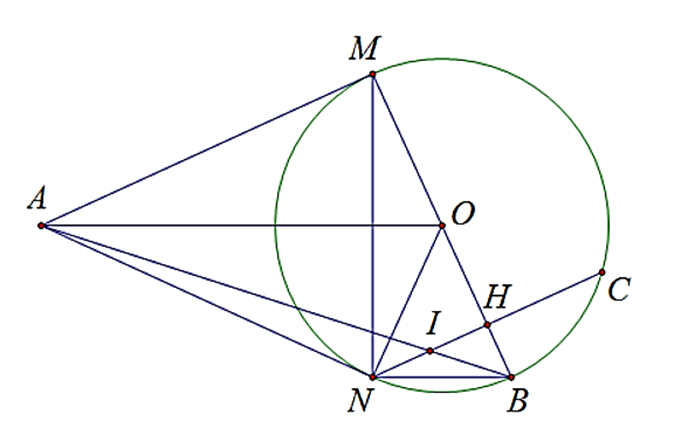
Ta có:

MA ⊥ MB (tiếp tuyến vuông góc với đường kính)

NC ⊥ OB suy ra: IH ⊥ MB

Do đó: IH // MA

Áp dụng định lí Thalès trong tam giác MAB có:

\(\frac{{HB}}{{MB}} = \frac{{IB}}{{BA}} = \frac{{IH}}{{MA}}\,\,hay\,\,\frac{{HI}}{{MA}} = \frac{{HB}}{{MB}} = \frac{{HB}}{{2MO}}\,\)(1)

Ta có: AMON là tứ giác nội tiếp đường tròn vì \[\widehat {ANO} + \widehat {AMO}\] = 180° suy ra: \[\widehat {MNO} = \widehat {MAO}\]

Mà \[\widehat {ONB}\, + \widehat {MON}\, = \widehat {MAO\,} + \,\widehat {MOA}\,\]= 90°

Suy ra: \[\widehat {ONB}\,\, = \,\,\widehat {MOA}\,\]

Mặt khác tam giác ONB cân tại O nên \[\widehat {ONB}\,\, = \,\,\widehat {HBN}\,\]

Xét tam giác HBN và tam giác MOA có:

\(\widehat {NHB} = \widehat {AMO}\)= 90°

\(\widehat {HBN} = \widehat {ONB} = \widehat {MOA}\)

Suy ra: ∆HBN ᔕ ∆MOA (g.g)

Hay \(\frac{{HN}}{{MA}} = \frac{{HB}}{{MO}} = \frac{{2HB}}{{MB}}\,\,\)(2)

Từ (1) và (2) suy ra: \(\frac{{HN}}{{MA}} = \frac{{2HI}}{{MA}}\,\,\)hay HN = 2HI = 2NI

Mà NC = 2HN

Suy ra: NC = 4NI

Vậy \[\frac{{NI}}{{NC}} = \frac{1}{4}\].