Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA.
a) Chứng minh tứ giác ADME là hình bình hành.
b) Nếu tam giác ABC cân tại A thì tứ giác ADME là hình gì? Vì sao?
c) Nếu tam giác ABC vuông tại A thì tứ giác ADME là hình gì? Vì sao?
d) Trong trường hợp tam giác ABC vuông tại A, cho biết AB = 6 cm, AC = 8 cm. Tính AM.
Quảng cáo
1 câu trả lời 90
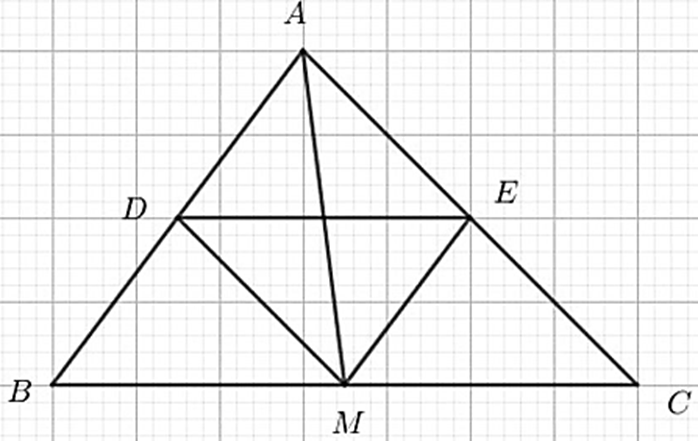
a) Ta có: EM là đường trung bình của tam giác ABC
Suy ra: EM // AB và EM = \(\frac{1}{2}AB\)= AD
Xét tứ giác ADME có: AD // ME và AD = ME
Suy ra tứ giác ADME là hình bình hành.
b) Nếu tam giác ABC cân tại A thì AE = AD = \(\frac{1}{2}AB\)=\(\frac{1}{2}AC\)
Suy ra: ADME là hình thoi vì AD = AE = ME = MD
c) Nếu tam giác ABC vuông tại A thì \(\widehat {EAD}\) = 90°
Suy ra: ADME là hình chữ nhật.
d) Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
BC = \(\sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + 8{}^2} = 10\)(cm)
Vì tam giác ABC vuông tại A nên đường trung tuyến bằng nửa cạnh huyền hay
AM = \(\frac{1}{2}BC\)= 5(cm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



