Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho BD = CE.
Chứng minh ∆ADE cân.
Quảng cáo
1 câu trả lời 91
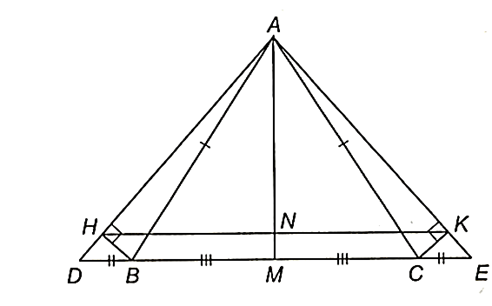
Do ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
Suy ra \[\widehat {ABD} = \widehat {ACE}\](cùng bù với gióc \[\widehat {ABC},\widehat {ACB}\]).
Xét ∆ABD và ∆ACE có:
AB = AC (do tam giác ABC cân tại A)
\[\widehat {ABD} = \widehat {ACE}\] (chứng minh trên),
Mà BD = CE (theo giả thiết).
Suy ra ∆ABD = ∆ACE (c.g.c),
Do đó AD = AE (hai cạnh tương ứng),
Suy ra tam giác ADE cân tại A.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340
Gửi báo cáo thành công!



