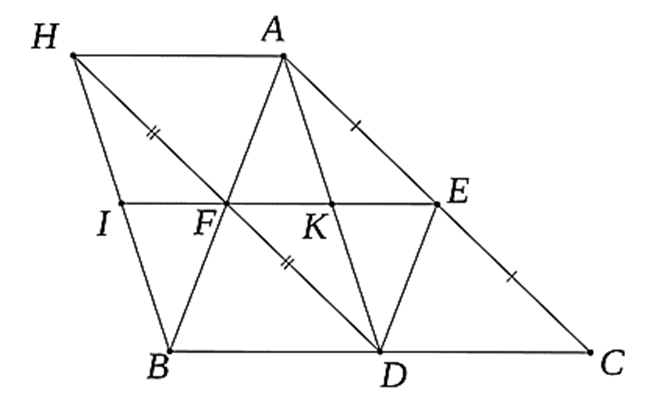
a)

Xét tứ giác BDEF có:

EF // BD (vì EF // BC)

ED // FB (vì ED // AB)

Do đó tứ giác BDEF là hình bình hành (tứ giác có cặp cạnh đối song song)

Tam giác ABC có:

EA = EC (gt)

ED // AB (gt)

Do đó DB = DC hay D là trung điểm của đoạn thẳng BC.

b)

Vì H đối xứng D qua F

⇒ F là trung điểm của HD (1)

Vì E là trung điểm của AC và EF // BC

⇒ F là trung điểm của AB (2)

Từ (1) và (2) ta có tứ giác HABD có hai đường chéo cắt nhau tại trung điểm mỗi đường.

⇒ AHBD là hình hình hành

⇒ HB // AD.

c)

Xét tam giác ∆HBD có:

I là trung điểm của HB

F trung điểm của HD

⇒ IF // BD (3)

Mà FE // BD (4)

⇒ I, F, E thẳng hàng.

⇒ I, K, E thẳng hàng.

d) Để HF = \(\frac{{AB}}{2}\) thì \(\frac{{HD}}{2} = \frac{{AB}}{2}\)

⇒ HD = AB

Hình bình hành AHBD có HD = AB

⇒ AHBD là hình chữ nhật

⇒ AD vuông góc với BC

Xét tam giác ABC có AD vừa là đường cao vừa là đường trung tuyến (D là trung điểm của BC)

⇒ ΔABC cân tại A.

Vậy ∆ABC cân tại A thì HF = \(\frac{{AB}}{2}\).