Cho hình bình hành ABCD, có \[\widehat A = 60^\circ \]. Lấy các điểm E, F theo thứ tự thuộc cạnh AD, CD sao cho DE = CF. Gọi K là điểm đối xứng với F qua BC. Chứng minh EK // AB.
Quảng cáo
1 câu trả lời 249
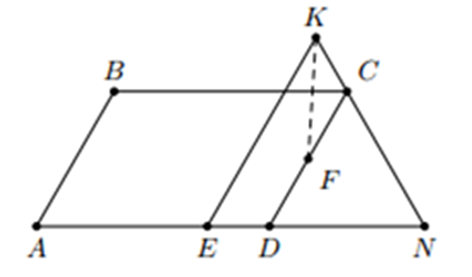
Kéo dài KC cắt AD tại N
Ta có AB // CD nên \[\widehat {BA{\rm{D}}} = \widehat {C{\rm{D}}N} = 60^\circ \]
K đối xứng với F qua BC nên \[\widehat {BC{\rm{D}}} = \widehat {KCB} = 60^\circ \]
\[\widehat {CN{\rm{D}}} = \widehat {KCB} = 60^\circ \]
⇒ Tam giác CND đều ⇒ CN = DN
Lại có CK = DE (cùng = CF)
KN = EN ⇒ tam giác KNE đều
⇒ \[\widehat {KEN} = \widehat {C{\rm{D}}N} = 60^\circ \]
⇒ KE // CD // AB
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340
Gửi báo cáo thành công!



