Question

Đã trả lời bởi chuyên gia

Answer 1

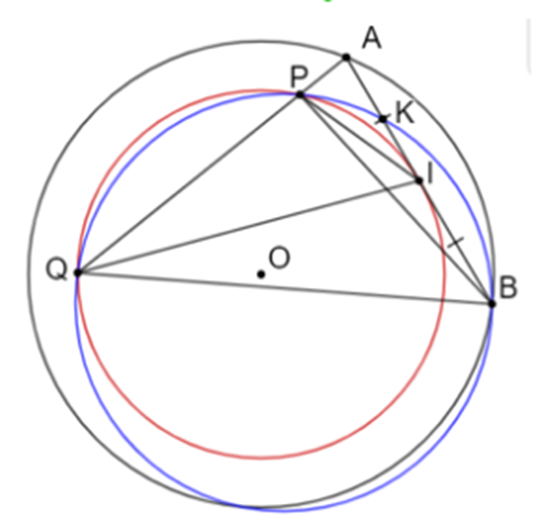
a) Xét (O; OA) có: \[IA = IB = \frac{1}{2}AB\]

⇒ OI ⊥ AB (mối quan hệ đường kính – dây cung)

⇒ OI ⊥ AI

Xét (O; OI) có: OI ⊥ AI

⇒ AI là tiếp tuyến của (O; OI) tại I

\[ \Rightarrow \widehat {PIA} = \widehat {PQI}\] (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn )

Hay \[\widehat {PIA} = \widehat {IQA}\]

Xét ∆AIP và ∆AQI có:

\[\widehat {PIA} = \widehat {IQA}\] (cmt)

\[\widehat A\] chung

Do đó ∆AIP ᔕ ∆AQI (g.g)

Suy ra \[\frac{{AI}}{{AQ}} = \frac{{AP}}{{AI}}\] (hai cạnh tương ứng tỉ lệ)

Do đó AP. AQ = AI².

b) Vì tứ giác BKPQ nội tiếp nên \[\widehat {APK} = \widehat {KBQ}\]

Hay \[\widehat {APK} = \widehat {ABQ}\]

Xét ∆APK và ∆ABQ có:

\[\widehat {APK} = \widehat {ABQ}\] (cmt)

\[\widehat A\]: góc chung

Do đó ∆APK ᔕ ∆ABQ (g. g)

Suy ra \[\frac{{AP}}{{AB}} = \frac{{AK}}{{AQ}}\] (hai cạnh tương ứng tỉ lệ)

Do đó AK . AB = AP . AQ.

...Xem thêm

Answer 2