Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.
Quảng cáo
1 câu trả lời 85
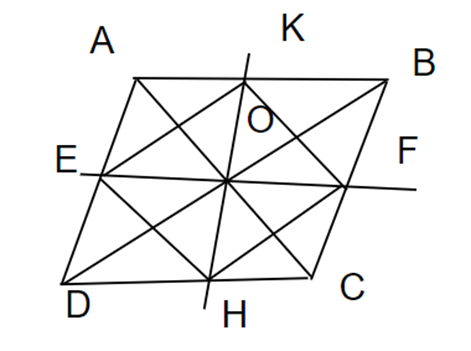
Vì ABCD là hình bình hành nên AB // CD
Suy ra: \(\widehat {ABD}\,\, = \,\,\widehat {BDC}\) (2 góc so le trong)
AD // BC nên \(\widehat {DAC}\,\, = \,\,\widehat {ACB}\) (2 góc sole trong)
Xét tam giác KOB và tam giác DOH có:
\(\widehat {ABD}\,\, = \,\,\widehat {BDC}\)
DO = OB
\(\widehat {DOH}\,\, = \,\,\widehat {BOK}\) (2 góc đối đỉnh)
Suy ra: ∆KOB = ∆DOH (g.c.g)
Nên OK= OH (2 cạnh tương ứng) (1)
Xét tam giác AEO và tam giác COF có:
\(\widehat {DAC}\,\, = \,\,\widehat {ACB}\)
AO = OC
\(\widehat {AOE}\,\, = \,\,\widehat {FOC}\) (2 góc đối đỉnh)
Suy ra: ∆AEO = ∆COF (g.c.g)
Nên EO = OF (2 cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OK = OH, EO = OF
⇒ EKFH là hình bình hành.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



