Cho hình bình hành ABCD. gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh M đối xứng với N qua O.
b) Chứng tỏ rằng tứ giác AMCN là hình bình hành.
Quảng cáo
1 câu trả lời 108
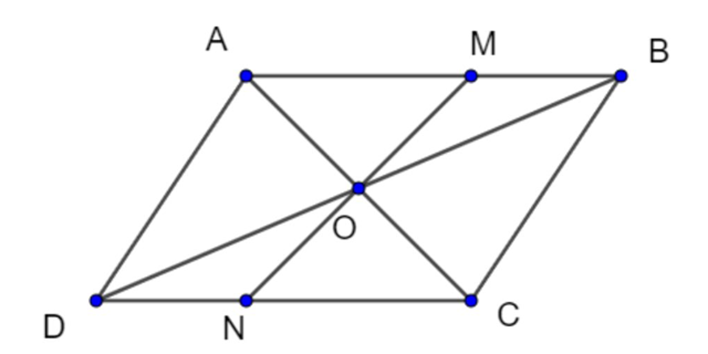
ABCD là hình bình hành
⇒AB // CD; O là trung điểm của AC.
⇒ OA = OC; \(\widehat {MAO}\, = \,\widehat {NCO}\) (so le trong)
Xét ΔMAO và ΔNCO có:
\(\widehat {MAO}\, = \,\widehat {NCO}\)
OA = OC
\(\widehat {MOA}\, = \,\widehat {NOC}\) (đối đỉnh)
⇒ ΔMAO ᔕ ΔNCO (g.c.g)
⇒ OM = ON
⇒ O là trung điểm của MN
Vậy M đối xứng với N qua O.
b) ΔMAO ᔕ ΔNCO
⇒ \(\frac{{AM}}{{CN}}\,\, = \,\,\frac{{OM}}{{ON}}\)
Mà OM = ON nên AM = CN
AB // CD ⇒ AM // CN
Xét tứ giác AMCN có:
AM // CN; AM = CN
⇒ AMCN là hình bình hành.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



