Cho nửa đường tròn (O) đường kính AB. Gọi E là 1 điểm nằm ngoài đường tròn. Tia AE và tia BE cắt đường tròn (O) tại C và D. AD cắt BC tại H.
a) Chứng minh: \(\widehat {AEH} = \widehat {ABH}\).
b) Biết \[\widehat {EAB}\]= 75° và \(\widehat {EBA}\)= 55°. Tính \(\widehat {COD}\).
Quảng cáo
1 câu trả lời 62
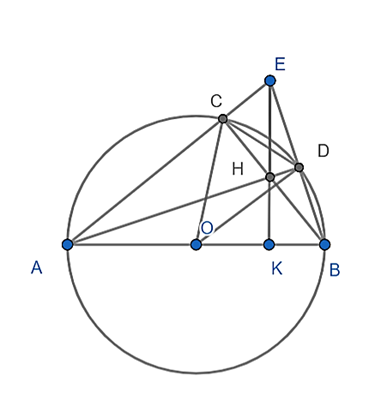
Ta có: \(\widehat {ACB} = \widehat {ADB}\)= 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra: AD ⊥ EB và BC ⊥ AE hay H là trực tâm của tam giác EAB.
⇒ EH ⊥ AB tại K (K là giao điểm của EH và AB).
\(\widehat {AEH} = \widehat {ABH}\)(cùng phụ với \(\widehat {EAB}\))
b) OA = OC = R suy ra tam giác OAC cân tại O.
\(\widehat {AOC} = \frac{{100^\circ - \widehat {EAB}}}{2} = 52,5^\circ \)
Tương tự: \(\widehat {DOB} = \frac{{100^\circ - \widehat {EBA}}}{2} = 62,5^\circ \)
\(\widehat {COD} = 180^\circ - \,\widehat {AOC} - \widehat {DOB} = 65^\circ \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



