Cho hình thang OABC, M, N lần lượt là trung điểm của OB và OC. Chứng minh rằng: \[\overrightarrow {AM} = \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \]và \[\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {OC} - \overrightarrow {OB} \,} \right)\].
Quảng cáo
1 câu trả lời 139
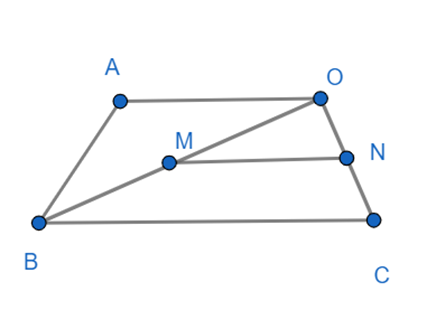
Ta có:
\[\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AO} + \overrightarrow {AB} } \right)\]
⇔ \[\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AO} + \overrightarrow {AO} + \overrightarrow {OB} } \right)\]
⇔ \[\overrightarrow {AM} = \frac{1}{2}\left( {2\overrightarrow {AO} + \overrightarrow {OB} } \right)\]
⇔ \[\overrightarrow {AM} = \overrightarrow {AO} \, + \,\frac{1}{2}\overrightarrow {OB} \, = \,\frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \]
Ta có: MN là đường trung bình của tam giác OCB.
Suy ra: \[\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} \]
⇔ \[\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {OC} - \overrightarrow {OB} \,} \right)\].
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



