Giả sử ABC là tam giác nhọn nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a, BC song song với DE.
b, Tứ giác BCED là hình thang cân.
Quảng cáo
1 câu trả lời 94
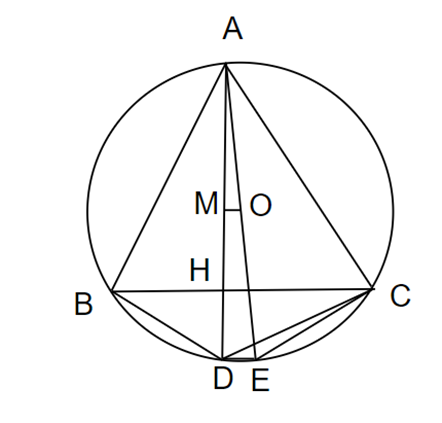
a) Từ O kẻ OM vuông góc với AD
Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD
Lại có O là trung điểm AE ⇒ MO là đường trung bình của tam giác ADE
⇒ MO // DE , lại có MO // BC (cùng vuông góc với AD)
⇒ DE // BC.
b) Tứ giác ABDC nội tiếp đường tròn (O) suy ra \[\widehat {ADB} = \widehat {BCA}\]
hay 90° – \(\widehat {ADB}\)= 90° – \(\widehat {BCA}\)
Suy ra: \(\widehat {CBD} = \widehat {ECB}\)
Theo phần a, vì BC // DE nên BCDE là hình thang
Vậy: BCDE là hình thang cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



