Cho tam giác ABC vuông tại A.Vẽ (O) đường kính AC.Đường tròn (O) cắt BC tạo điểm thứ hai là I. Kẻ OM vuông góc BC tại M. AM giao (O) tại điểm thứ hai là N. Chứng minh tam giác AIM đồng dạng tam giác CNM.
Quảng cáo
1 câu trả lời 78
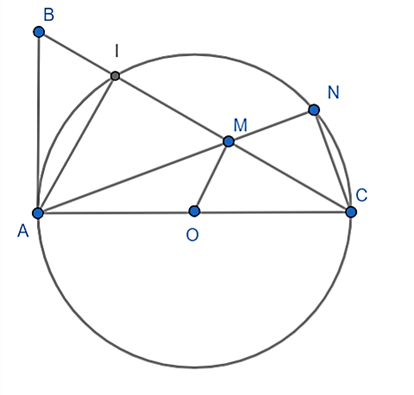
Ta thấy O là trung điểm AC, OM // AI (Cùng vuông góc với BC) nên OM là đường trung bình tam giác AIC.
Suy ra: M là trung điểm của IC hay IM = MC
Xét tam giác AIM và tam giác CNM có
\[\widehat {IMA}\, = \,\widehat {NMC}\](hai góc đối đỉnh)
\[\widehat {AIM}\, = \,\widehat {CNM}\](hai góc nội tiếp cùng chắn cung AC)
Suy ra: ΔAIM ᔕ ΔCNM (g−g).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340
Gửi báo cáo thành công!



