Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn (D nằm giữa A và E). Tia phân giác góc \(\widehat {DBE}\)cắt DE tại I. Chứng minh rằng:
a) \(\frac{{BD}}{{BE}} = \frac{{AD}}{{AB}}\).
b) \(\frac{{BD}}{{BE}} = \frac{{CD}}{{CE}}\).
Quảng cáo
1 câu trả lời 120
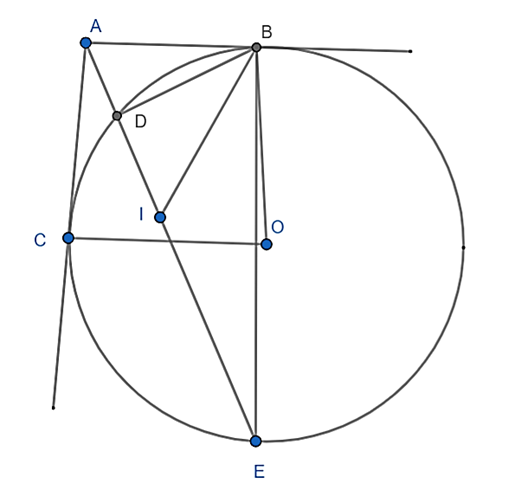
a) Xét tam giác ADB và tam giác ABE có:
\(\widehat A\)chung
\(\widehat {ABD} = \,\widehat {AEB}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung, đều bằng \(\frac{1}{2}\)cung BD)
Suy ra: ∆ADB ᔕ ∆ABE (g.g)
⇒ \(\frac{{BD}}{{BE}} = \frac{{AD}}{{AB}}\)
b) Theo câu a ta có: ∆ADB ᔕ ∆ABE (g.g)
⇒ \(\frac{{BD}}{{BE}} = \frac{{AB}}{{AE}}\)(1)
Xét ∆ADC và ∆ACE có:
\(\widehat A\) chung
\(\widehat {ACD} = \,\widehat {AEC}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung, đều bằng \(\frac{1}{2}\)cung BD)
Suy ra: ∆ADC ᔕ ∆ACE (g.g)
⇒ \(\frac{{CD}}{{CE}} = \frac{{AC}}{{AE}}\)
Mà AB = AC (tính chất 2 tiếp tuyến cắt nhau) (3)
Từ (1), (2) và (3) suy ra: \(\frac{{BD}}{{BE}} = \frac{{CD}}{{CE}}\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



