Quảng cáo
1 câu trả lời 87
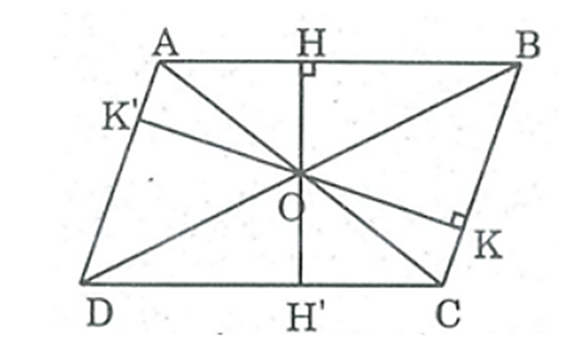
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2 cm , đến cạnh BC là OK = 3 cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2 cm
Suy ra HH' bằng đường cao của hình bình hành.
SABCD = HH'.AB ⇒ AB = \(\frac{{{S_{ABCD}}}}{{HH'}}\,\, = \,\,\frac{{24}}{4}\,\, = \,\,6\) (cm)
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ AD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
SABCD = KK'.BC ⇒ BC = \(\frac{{{S_{ABCD}}}}{{KK'}}\,\, = \,\,\frac{{24}}{6}\,\, = \,\,4\)(cm)
Chu vi của hình bình hành ABCD là: (6 + 4) . 2 = 20 (cm).
Đáp số: 20 cm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



