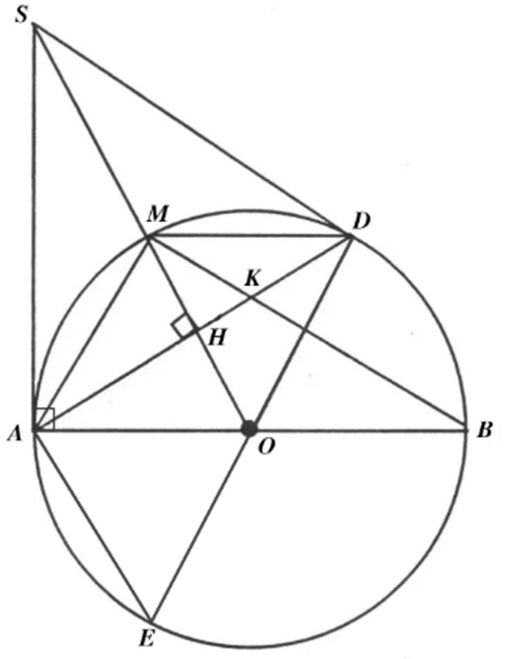
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1. Chứng minh SD là tiếp tuyến của đường tròn (O).
2. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3. Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH.KD\).
Quảng cáo
1 câu trả lời 251
1.
Xét tam giác OAB có:
OA = OD = R
OH vuông góc với AD
Do đó, tam giác OAD cân tại O có OH là đường cao
Do đó, OH là phân giác của góc \(\widehat {AOD}\)
\( \Rightarrow \widehat {SOA} = \widehat {SOD}\)
Xét tam giác SAO và tam giác SDO có:
KO chung
\(\widehat {SOA} = \widehat {SOD}\)
OA = OD = R
Do đó, tam giác SAO bằng tam giác SDO (c.g.c)
\( \Rightarrow \widehat {SDO} = \widehat {SAO} = 90^\circ \)
Hay SD vuông góc với OD
Do đó, SD là tiếp tuyến của (O) tại D.
2,
Xét tam giác OAM có OA = OM
Do đó, tam giác OAM cân tại O
\( \Rightarrow \widehat {OAM} = \widehat {AMH}\)
Mà \(\widehat {OAM} + \widehat {SAM} = \widehat {SAO} = 90^\circ \)
Và \(\widehat {AMH} + \widehat {HAM} = 90^\circ \)
\( \Rightarrow \widehat {SAM} = \widehat {HAM}\)
Do đó, AM là đường phân giác của tam giác SAD (1)
Mặt khác SA, SD là các tiếp tuyến của đường tròn (O)
Do đó, SO là tia phân giác của \(\widehat {ASD}\)(2)
Từ (1) và (2) ta có: M là tâm đường tròn nội tiếp tam giác SAD.
Mà MH vuông góc với AD tại H nên MH là bán kính đường tròn nội tiếp tam giác SAD.
Do đó, MH = r, OH = R – r
Xét tam giác AOH vuông tại H
Ta có: OA2 = OH2 + AH2 (định lý Py–ta–go)
\( \Rightarrow AH = \sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \Rightarrow AD = 2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \)
Ta có: \(\widehat {EAD}\) chắn đường kính DE \( \Rightarrow \widehat {EAD} = 90^\circ \)
Xét tam giác EAD vuông tại A có:
DE2 = AD2 + AE2 (định lý Py–ta–go)
\( \Rightarrow AE = \sqrt {4{{\left( {R - r} \right)}^2}} = 2\left( {R - r} \right)\).
3.
OH là đường trung trực của AD, M thuộc OH
Do đó, DM = AM = R
Tứ giác AMDO có AM = MD = OA = OD (= R)
Tứ giác AMDO là hình thoi
Do đó, AM song song với DO.
Mà AM vuông góc với BM , BM vuông góc với OD
Tam giác OMD có OM = OD = CD (= R)
Do đó, tam giác OMD đều
Mà MB, DM là hai đường cao cắt nhau tại K của tam giác OMD
Do đó, K là trực tâm của tam giác đều OMD
Do đó, K là trọng tâm của tam giác đều OMD
\(KH = \frac{1}{3}DH;KD = \frac{2}{3}DH \Rightarrow KH.KD = \frac{2}{9}D{H^2}\)
Mà tam giác HMD vuông tại H
Do đó, DH = \(DH = MD.\sin 60^\circ = \frac{{\sqrt 3 }}{2}MD \Rightarrow MD = \frac{2}{{\sqrt 3 }}DH\)
\( \Rightarrow M{D^2} = 6.\frac{2}{9}D{H^2} = 6.KH.KD \Rightarrow \frac{{M{D^2}}}{6} = KH.KD\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



