Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD.
a) CMR: \(\widehat {AMN} = 90^\circ \). Từ đó suy ra bốn điểm A, M, N, D cùng thuộc một đường tròn.
b) So sánh AN và MD.
Quảng cáo
1 câu trả lời 83
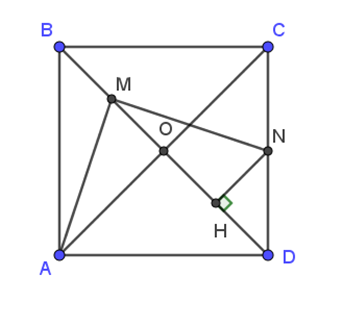
a)
Kẻ NH vuông góc với DO
Ta có ABCD là hình vuông ⇒ AC vuông góc với BD
Mà N là trung điểm của DC, NH vuông góc với DO
⇒ NH \({\rm{//}}\) OC
Do đó, NH là đường trung bình
Mà M là trung điểm OB (gt)
Suy ra H là trung điểm OD
\(NH = \frac{1}{2}OC = OM\)
Suy ra HM = OA
Xét tam giác OMA và tam giác HNM có:
\(\widehat H = \widehat O = 90^\circ \)
NH = MO
HM = OA
Do đó tam giác OMA và tam giác HNM bằng nhau
\( \Rightarrow \widehat {OAM} = \widehat {HMN}\)
\( \Rightarrow \widehat {AMN} = \widehat {AMO} + \widehat {HMN} = \widehat {AMO} + \widehat {OAM} = 90^\circ \) (đcpcm).
Gọi I là trung điểm của AN
Tam giác AMN vuông tại M ⇒ \(MI = \frac{1}{2}AN = AI\)
Tam giác ADN vuông tại D ⇒ \(DI = \frac{1}{2}AN = AI\)
Suy ra IA = IM = IN = ID
Do đó, 4 điểm A, M, N, D cùng thuộc đường tròn tâm I.
b)
Xét đường tròn ngoại tiếp tứ giác AMND
Có AN là đường kính và DM là dây nên AN > DM.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



