Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC = AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng: MA2 = MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM song song với EF.
Quảng cáo
1 câu trả lời 67
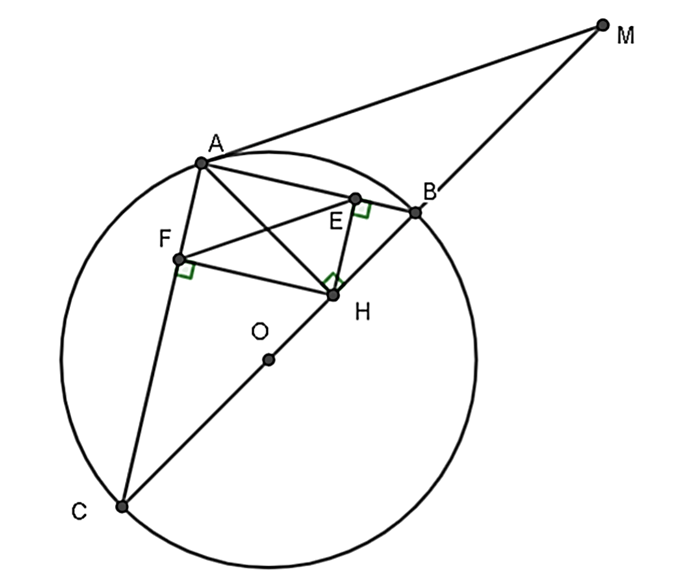
Xét tam giác ABC có:
\(\widehat {BAC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Do đó, tam giác ABC vuông tại A
\({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AB.AC\)
\( \Rightarrow AH.BC = AB.AC\).
b)
Xét tam giác MAB và tam giác MCA có:
\(\widehat M\) chung
\(\widehat {MAB} = \widehat {MCA}\)(cùng chắn cung AB)
Do đó, tam giác MAB đồng dạng với tam giác MCA (g.g)
\( \Rightarrow \frac{{MA}}{{MC}} = \frac{{MB}}{{MA}} \Rightarrow M{A^2} = MC.MB\).
c)
AM vuông góc với AO (do AM là tiếp tuyến của (O))
Xét tam giác AOC có:
AO = OC
Do đó, tam giác AOC cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Mà \(\widehat {AFE} = \widehat {ABC}\)
\(\widehat {OCA} + \widehat {ABC} = 90^\circ \)
\( \Rightarrow \widehat {OAC} + \widehat {AFE} = 90^\circ \)
Do đó, AO vuông góc với EF
Do đó, EF song song với AM.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



