Cho đường tròn (O ; R) và một điểm A sao cho OA = 2R vẽ các tiếp tuyến AB, AC với (O; R) , B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.
b) Chứng minh DC song song với OA.
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh OCEA là hình thang cân.
Quảng cáo
1 câu trả lời 287
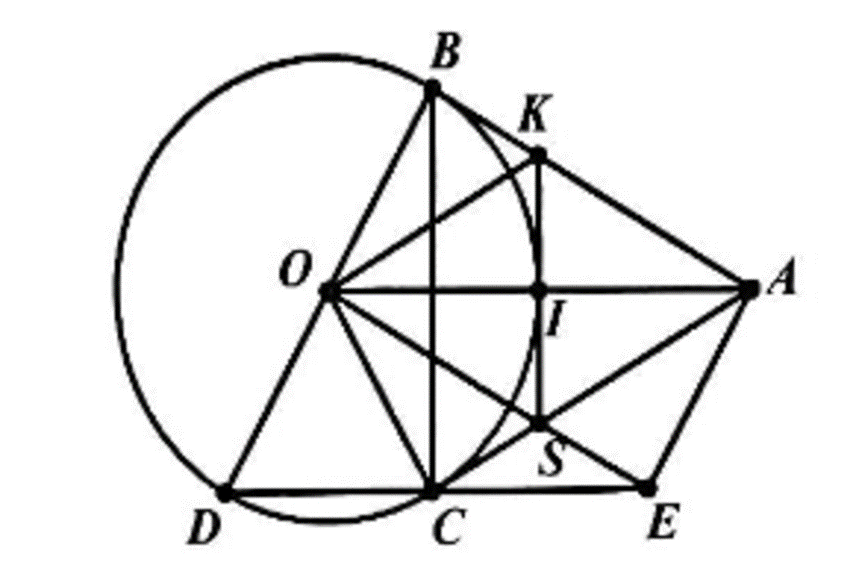
a)
AB, AC là các tiếp tuyến của (O) nên \(\widehat {OBA} = \widehat {OCA} = 90^\circ \)
Do đó, B, C cùng thuộc một đường tròn đường kính OA
Do đó, A, B, C, O cùng thuộc đường tròn đường kính OA
b)
AB, AC là tiếp tuyến của (O) nên AB = AC mà OC = OB = R
Do đó, OA là trung trực của BC
Nên OA vuông góc với BC
Tam giác BCD nội tiếp đường tròn (O; R) nên \(\widehat {BCD} = 90^\circ \) hay DC vuông góc với BC
Do đó, CD song song với OA (cùng vuông góc với BC)
c)
DC song song với OA nên CE song song với OA
Do đó, OCEA là hình thang
Ta có: tam giác ODE bằng tam giác BOA (g.c.g) nên OE = AB
⇒ OE = AC
Do đó, OCEA là hình thang cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



