Cho 2 đường thẳng xx' và yy' song song với nhau. Đường thẳng a cắt xx', yy' lần lượt tại A và B. Tia At là tia phân giác của \[\widehat {xAB}\].
a) Chứng minh tia At cắt đường thẳng yy'.
b) Cho \[\widehat {xAB} = 70^\circ \], At cắt yy' tại C. Tính số đo góc ACB.
Quảng cáo
1 câu trả lời 52
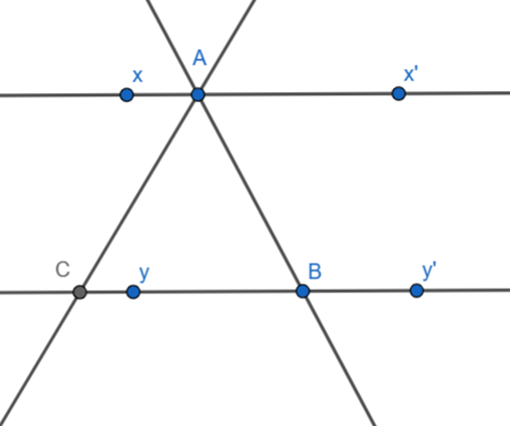
a) Nếu tia At không cắt yy'
Þ At // yy'
Þ At trùng với Ax (vì xx' // yy')
Mà At là phân giác \[\widehat {xAB}\]
Þ At nằm giữa Ax và AB
Þ At không trùng Ax
Þ At cắt yy' (đpcm).
b) Ta có \[\widehat {xAC} = \widehat {ACB}\] (hai góc so le trong do xx' // yy').
mà \[\widehat {xAC} = \frac{{\widehat {xAB}}}{2} = \frac{{70^\circ }}{2} = 35^\circ \] (do AC là tia phân giác của \[\widehat {xAB}\]).
Þ \[\widehat {ACB} = 35^\circ \] (đpcm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



